Cho tứ diện OABC có OA vuông góc với mặt phẳng (OBC) và có A′, B′, C′ lần lượt là trung điểm của OA
26
31/10/2024
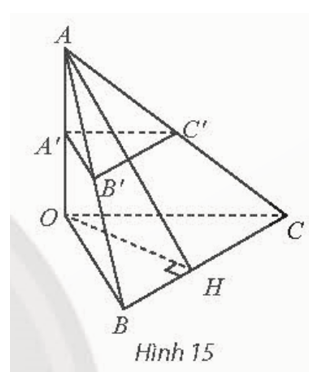
Cho tứ diện OABC có OA vuông góc với mặt phẳng (OBC) và có A′, B′, C′ lần lượt là trung điểm của OA, OB, OC. Vẽ OH là đường cao của tam giác OBC. Chứng minh rằng:
a) OA ⊥ (A′B′C′);
Trả lời
a) Xét tam giác OAB:
A′ là trung điểm OA
B′ là trung điểm AB
Nên A′B′ là đường trung bình của ΔOAB.
Do đó A′B′ // OB A′B′ // (OBC) (vì
Tương tự: B′C′ là đường trung bình của ΔABC
Do đó B′C′ // BC B′C′ // (OBC) (vì
Ta có:
Mà OA ⊥ (OBC)
Vậy OA ⊥ (A′B′C′).