Bài 4.16 trang 59 SBT Toán 11 Tập 1: Cho tứ diện ABCD. Gọi M, N, P, Q lần lượt là trung điểm của các cạnh AB, BC, CD, DA.
a) Xác định giao tuyến của hai mặt phẳng (ANP) và (CMQ).
b) Xác định giao tuyến của hai mặt phẳng (ANP) và (ABD).
c) Xác định giao tuyến của hai mặt phẳng (CMQ) và (BCD).
d) Chứng minh rằng các giao tuyến ở trên đôi một song song với nhau.
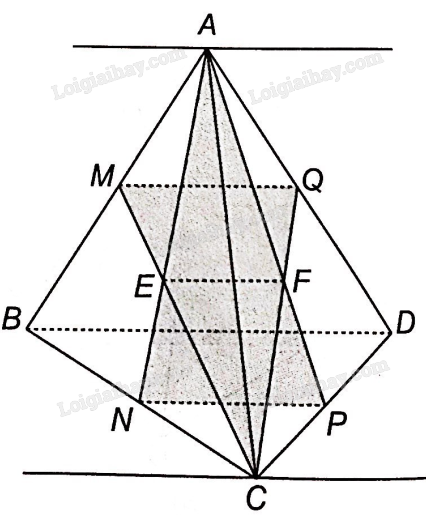
a) M, Q lần lượt là trung điểm của các cạnh AB, DA nên MQ là đường trung bình tam giác ABD nên MQ//BD.
N, P lần lượt là trung điểm của các cạnh BC, CD nên NP là đường trung bình tam giác CBD nên NP//BD.
Vậy MQ//NP, suy ra M, N, P, Q đồng phẳng.
Xét 3 mặt phẳng (MNPQ), (ANP) và (CMQ).
MQ là giao tuyến của (MNPQ) và (CMQ).
NP là giao tuyến của (MNPQ) và (ANP).
Vậy giao tuyến của (ANP) và (CMQ) cũng là một đường thẳng song song với MQ và NP.
Trong mặt phẳng (ABC), gọi E là giao điểm của AN và MC. Trong mặt phẳng (ACD) gọi F là giao điểm của CQ và AP. Vậy EF là giao tuyến của hai mặt phẳng (ANP) và (CMQ).
b)
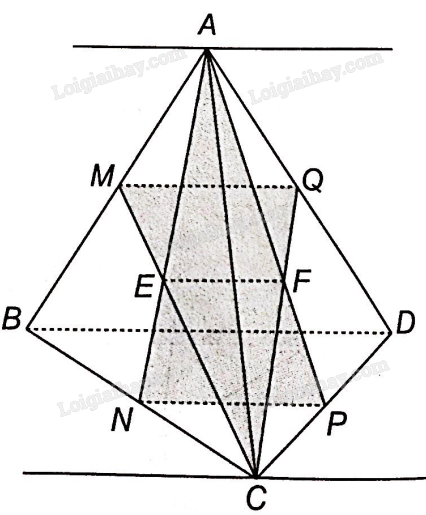
Xét 3 mặt phẳng (BCD), (ANP) và (ABD).
BD là giao tuyến của (BCD) và (ABD).
NP là giao tuyến của (BCD) và (ANP).
Mà theo chứng minh trên, BD//NP.
Vậy giao tuyến của (ANP) và (ABD) cũng là một đường thẳng song song với BD và NP.
Mà A là điểm chung của hai mặt phẳng (ANP) và (ABD) , vậy giao tuyến của hai mặt phẳng đó là đường thẳng đi qua A và song song với BD.
c)
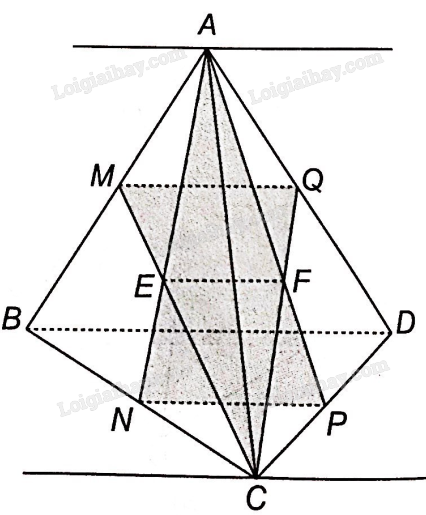
Xét 3 mặt phẳng (BCD), (ABD) và (CMQ).
MQ là giao tuyến của (ABD) và (CMQ).
BD là giao tuyến của (BCD) và (ABD).
Mà MQ//BD nên giao tuyến của mặt phẳng (CMQ) và (BCD) cũng là một đường thẳng song song với MQ và BD.
Ta thấy C là một điểm chung của mặt phẳng (CMQ) và (BCD), vậy giao tuyến của hai mặt phẳng (CMQ) và (BCD) là đường thẳng đi qua C và song song với BD.
d) Theo chứng minh trên, các đường giao tuyến đều song song với MQ, NP, BD nên chúng song song với nhau.
Xem thêm các bài giải SBT Toán lớp 11 Kết nối tri thức hay, chi tiết khác:
Bài 10: Đường thẳng và mặt phẳng trong không gian
Bài 11: Hai đường thẳng song song
Bài 12: Đường thẳng và mặt phẳng song song