Cho tứ diện ABCD có (ABD) ⊥ (BCD) và CD ⊥ BD. Chứng minh rằng tam giác ACD vuông.

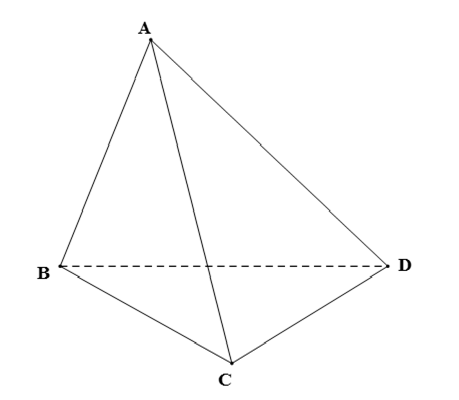
Vì B ∈ (ABD) ∩ (BCD);

     D ∈ (ABD) ∩ (BCD).

Suy ra BD = (ABD) ∩ (BCD).

Ta có: (ABD) ⊥ (BCD);

           (ABD) ∩ (BCD) = BD;

           CD ⊂ (BCD) và CD ⊥ BD.

Suy ra CD ⊥ (ABD).

Mà AD ⊂ (ABD) nên CD ⊥ AD.

Vậy tam giác ACD vuông tại D.