Chứng minh các định lí sau:

a) Nếu hai mặt phẳng (phân biệt) cùng vuông góc với mặt phẳng thứ ba thì song song với nhau hoặc cắt nhau theo một giao tuyến vuông góc với mặt phẳng thứ ba đó;

a)

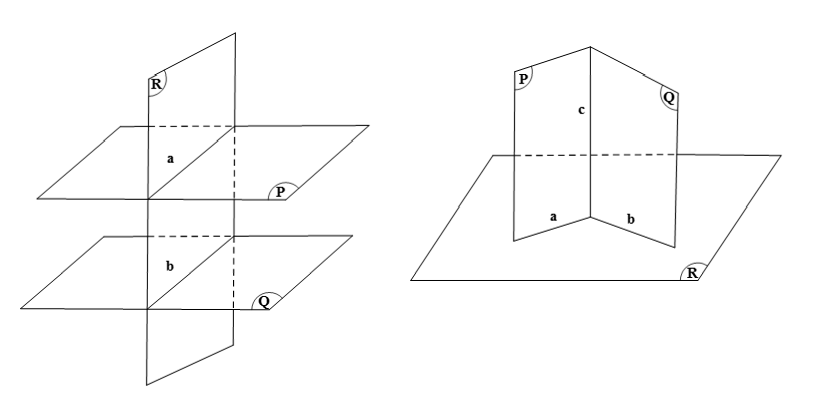
Giả sử ta có: (P) ⊥ (R), (Q) ⊥ (R), gọi a = (P) ∩ (R), b = (Q) ∩ (R).

Mà (P) và (Q) là hai mặt phẳng phân biệt nên a và b không trùng nhau.

Hơn nữa: a và b cùng nằm trong (R), nên xảy ra hai trường hợp:

⦁ Nếu a // b, mà a ⊂ (P), b ⊂ (Q) thì suy ra (P) // (Q).

⦁ Nếu a cắt b, mà a ⊂ (P) và b ⊂ (Q), thì ta gọi c = (P) ∩ (Q).

Do (P) ⊥ (R), (Q) ⊥ (R) và c = (P) ∩ (Q) nên suy ra c ⊥ (R).