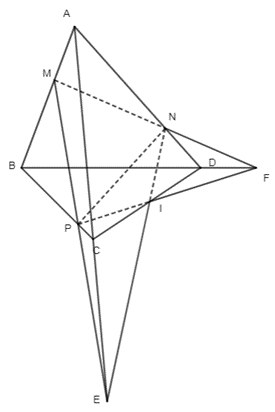
Cho tứ diện ABCD. Các điểm M, N, P lần lượt thuộc các cạnh AB, AD, BC sao cho \(\frac{{AM}}{{AB}} = \frac{1}{3},\frac{{AN}}{{AD}} = \frac{2}{3},\frac{{BP}}{{BC}} = \frac{3}{4}\).

a) Xác định E, F lần lượt là giao điểm của các đường thẳng AC, BD với mặt phẳng (MNP).

b) Chứng minh rằng các đường thẳng NE, PF và CD cùng đi qua một điểm.

Lời giải

a)

+) Trong mặt phẳng (ABC), gọi giao điểm của MP với AC là E.

Mà MP ⊂ (MNP) nên (MNP) ∩ AC = {E}.

+) Trong mặt phẳng (ABD), gọi giao điểm của MN với BD là F.

Mà MP ⊂ (MNP) nên (MNP) ∩ BD = {F}.

b) • Ta có: N ∈ AD, mà AD ⊂ (ACD) nên N ∈ (ACD).

Lại có N ∈ (MNP)

Do đó N là giao điểm của (ACD) và (MNP).

Mặt khác: MP ∩ AC = {E};

                 MP ⊂ (MNP);

                 AC ⊂ (ACD).

Do đó E là giao điểm của (ACD) và (MNP).

Suy ra NE = (MNP) ∩ (ACD).

Trong mặt phẳng (ACD), nối NE cắt CD tại I.

Khi đó I ∈ CD và I ∈ NE ⊂ (MNP)

• Ta có: P ∈ BC, mà BC ⊂ (BCD) nên P ⊂ (BCD)

Lại có P ∈ (MNP)

Do đó P là giao điểm của (BCD) và (MNP).

Mặt khác: MN ∩ BD = {F}.

                 MN ⊂ (MNP);

                 BD ⊂ (BCD) .

Do đó F là giao điểm của (BCD) và (MNP).

Suy ra PF = (BCD) ∩ (MNP).

Trong mặt phẳng (BCD), gọi giao điểm của CD với PF là I.

Khi đó I ∈ CD, mà CD ⊂ (ACD)

            I ∈ PF, mà PF ⊂ (MNP)

Suy ra I là giao điểm của hai mặt phẳng (MNP) và (ACD).

Hay I nằm trên giao tuyến NE của (MNP) và (ACD).

Do đó I ∈ NE.