Lời giải
a)
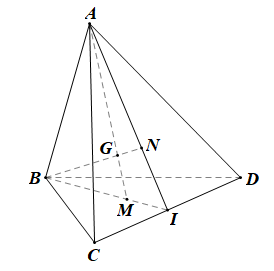
+) Xét tam giác BCD có: I là trung điểm của CD nên BI là đường trung tuyến.
Mà M là trọng tâm tam giác BCD nên BI đi qua M.
Do đó M ∈ BI.
Lại có AI ⊂ (ABI) nên M ∈ (ABI).
+) Xét tam giác ACD có: I là trung điểm của CD nên AI là đường trung tuyến.
Mà N là trọng tâm tam giác ACD nên AI đi qua N.
Do đó N ∈ AI.
Lại có BI ⊂ (ABI) nên N ∈ (ABI).
b) Trong DBCD có M là trọng tâm tam giác nên \(\frac{{MI}}{{BI}} = \frac{1}{3}\).
Trong DACD có N là trọng tâm tam giác nên \(\frac{{NI}}{{AI}} = \frac{1}{3}\).
Xét DABI có: \(\frac{{NI}}{{AI}} = \frac{{MI}}{{BI}} = \frac{1}{3}\) nên MN // AB (theo định lí Thalès đảo).
Xét DABI và MN // AB, theo hệ quả định lí Thalès ta có \(\frac{{MN}}{{AB}} = \frac{{NI}}{{AI}} = \frac{{MI}}{{BI}} = \frac{1}{3}\).
Xét DABG và MN // AB, theo hệ quả định lí Thalès ta có \(\frac{{GM}}{{GA}} = \frac{{GN}}{{GB}} = \frac{{MN}}{{AB}} = \frac{1}{3}\).
c)
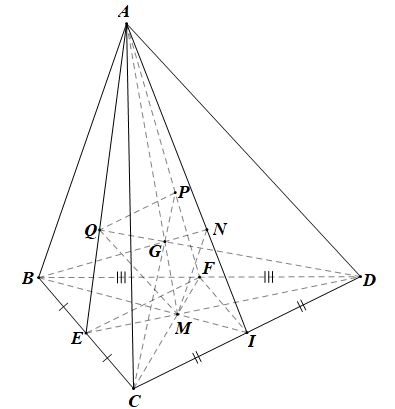
• Gọi G’ là giao điểm của AM và CP; G’’ là giao điểm của AM và DQ.
Chứng minh tương tự câu b, ta có: \(\frac{{G'M}}{{G'A}} = \frac{{G'P}}{{G'C}} = \frac{{PM}}{{AC}} = \frac{1}{3}\) và \(\frac{{G''M}}{{G''A}} = \frac{{G''Q}}{{G''D}} = \frac{{QM}}{{AD}} = \frac{1}{3}\)
Do đó \(\frac{{GM}}{{GA}} = \frac{{G'M}}{{G'A}} = \frac{{G''M}}{{G''A}} = \frac{1}{3}\).
Mà G, G’, G’’ cùng nằm trên AM nên G ≡ G’ ≡ G’’.
Vậy các đường thẳng CP, DQ cùng đi qua điểm G.
• Xét tam giác ABC, kẻ đường trung tuyến AE (E ∈ BC).
Ta có: Q là trọng tâm DABC nên \(\frac{{AQ}}{{AE}} = \frac{2}{3}\).
Xét tam giác ABD, kẻ đường trung tuyến AF (F ∈ BD).
Ta có: P là trọng tâm DABD nên \(\frac{{AP}}{{AF}} = \frac{2}{3}\).
+) Trong mặt phẳng (AEF), có: \(\frac{{AQ}}{{AE}} = \frac{{AP}}{{AF}} = \frac{2}{3}\) nên PQ // EF (định lí Thalès đảo)
Mà EF // CD (đường trung bình tam giác BCD).
Suy ra PQ // CD
Theo hệ quả định lí Thalès ta có: \(\frac{{GP}}{{GC}} = \frac{{GQ}}{{GD}} = \frac{{QP}}{{CD}} = \frac{{QP}}{{2EF}} = \frac{1}{2}.\frac{2}{3} = \frac{1}{3}\).
