Cho hình chóp tứ giác S.ABCD có đáy không là hình thang. Gọi M là trung điểm của SA.

a) Xác định giao điểm của CD với mặt phẳng (SAB).

b) Xác định giao tuyến của hai mặt phẳng (SAB) và (SCD).

c) Xác định giao tuyến của hai mặt phẳng (MCD) và (SBC).

Lời giải

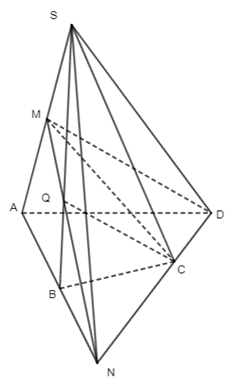
a) Trong mặt phẳng (ABCD) ta có: gọi giao điểm của AB và CD là N.

Mà AB ⊂ (SAB)

Do đó CD ∩ (SAB) = {N}.

b) Ta có: AB ∩ CD = {N};

               AB ⊂ (SAB);

               CD ⊂ (SCD)

Do đó N là giao điểm của (SAB) và (SCD).

Lại có: S ∈ (SAB) và S ∈ (SCD).

Nên S là giao điểm của (SAB) và (SCD).

Vì vậy (SAB) ∩ (SCD) = SN.

c) Ta có: C ∈ (SBC) và C ∈ (MCD).

Do đó C là giao điểm của (SBC) và (MCD).

Trong mặt phẳng (SAB), gọi Q là giao điểm của MN và SB.

Mà MN ⊂ (MCD) và SB ⊂ (SBC)  

Suy ra Q là giao điểm của (SBC) và (MCD).

Vì vậy (SBC) ∩ (MCD) = CQ.