Cho hình chóp S.ABCD có đáy là hình bình hành. Gọi M, N lần lượt là trung điểm của các cạnh SA và AD.
a) Xác định giao điểm của mặt phẳng (CMN) với các đường thẳng AB, SB.
b) Xác định giao tuyến của mặt phẳng (CMN) với mỗi mặt phẳng (SAB) và (SBC).
Lời giải
a)
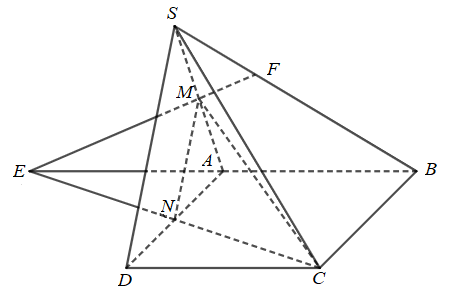
+) Trong mặt phẳng (ABCD): Gọi giao điểm của AB với NC là E.
Mà NC ⊂ (CMN)
Suy ra: (CMN) ∩ AB = {E}.
+) Trong mặt phẳng (SAB): Kéo dài EM cắt AB tại F.
Mà EM ⊂ (CMN)
Suy ra (SAB) ∩ EM = {F}.
b)
+) Ta có: M ∈ SA mà SA ⊂ (SAB) nên M ∈ (SAB);
M ∈ CM mà CM ⊂ (CMN) nên M ∈ (CMN).
Do đó M là giao điểm của hai mặt phẳng (SAB) và (CMN).
Ta lại có: AB ∩ CN = {E};
AB ⊂ (SAB);
CN ⊂ (CMN).
Do đó E là giao điểm của hai mặt phẳng (SAB) và (CMN).
Vì vậy (SAB) ∩ (CMN) = EM.
+) Ta có: C ∈ SC mà SC ⊂ (SBC);
C ∈ CM mà CM ⊂ (CMN).
Do đó C là giao điểm của hai mặt phẳng (SBC) và (CMN).
Ta lại có: SB ∩ EM = {F};
SB ⊂ (SBC);
EM ⊂ (CMN).
Do đó F là giao điểm của hai mặt phẳng (SBC) và (CMN).
Vì vậy (SBC) ∩ (CMN) = CF.