Lời giải
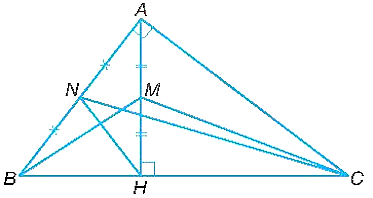
Tam giác ABC vuông tại A và tam giác HAC vuông tại H có: \(\widehat {ACB}\) chung.
Do đó, ∆ABC ᔕ ∆HAC (góc nhọn).
Suy ra \(\frac{{BC}}{{CA}} = \frac{{AB}}{{HA}} = \frac{{2BN}}{{2AM}} = \frac{{BN}}{{AM}}\) (do M, N lần lượt là trung điểm của AH, AB).
Hay \(\frac{{AC}}{{CB}} = \frac{{AM}}{{BN}}\).
Xét tam giác CAM và tam giác CNB có:
\(\widehat {CAM} = \widehat {CBN}\,\,\,\,\left( { = 90^\circ - \widehat {BAH}} \right)\)
\(\frac{{AC}}{{CB}} = \frac{{AM}}{{BN}}\) (cmt)
Do đó, ∆CAM ᔕ ∆CBN (c.g.c).
Vì ∆ABC ᔕ ∆HAC nên ta có: \(\frac{{AC}}{{HC}} = \frac{{AB}}{{AH}} = \frac{{2AN}}{{2HM}} = \frac{{AN}}{{HM}}\) hay \(\frac{{HC}}{{AC}} = \frac{{HM}}{{AN}}\).
Xét tam giác CHM vuông tại H và tam giác CAN vuông tại A có:
\(\frac{{HC}}{{AC}} = \frac{{HM}}{{AN}}\) (cmt)
Do đó, ∆CHM ᔕ ∆CAN (hai cạnh góc vuông).