Cho tam giác ABC vuông tại A có đường cao AH. Gọi M, N, P lần lượt là trung điểm của HA, HB, HC. Chứng minh rằng:
a) ∆MNP ᔕ ∆ABC và tìm tỉ số đồng dạng.
b) ∆ABN ᔕ ∆CAM và ∆ACP ᔕ ∆BAM.
c) AN ⊥ CM và AP ⊥ BM.
Lời giải
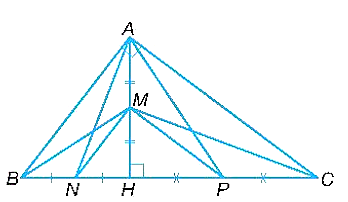
a) Tam giác CAH có P, M lần lượt là trung điểm của CH, AH nên MP là đường trung bình của tam giác ACH, suy ra \(\frac{{MP}}{{AC}} = \frac{1}{2}\).
Tam giác BAH có N, M lần lượt là trung điểm của BH, AH nên MN là đường trung bình của tam giác ABH, suy ra \(\frac{{MN}}{{AB}} = \frac{1}{2}\).
Ta có \(\frac{{PN}}{{CB}} = \frac{{PH + HN}}{{CH + HB}} = \frac{{PH + HN}}{{2\left( {PH + HN} \right)}} = \frac{1}{2}\) (do N, P lần lượt là trung điểm của HB, HC).
Tam giác MNP và tam giác ABC có:
\(\frac{{MP}}{{AC}} = \frac{{PN}}{{CB}} = \frac{{MN}}{{AB}} = \frac{1}{2}\).
Nên ∆MNP ᔕ ∆ABC (c.c.c) với tỉ số đồng dạng bằng \(\frac{1}{2}\).
b)
Tam giác ABH vuông tại H và tam giác HAC vuông tại H có:
\(\widehat {ABH} = \widehat {CAH}\,\,\,\,\left( { = 90^\circ - \widehat {ACH}} \right)\)
Do đó, ∆HBA ᔕ ∆HAC (góc nhọn).
Suy ra \(\frac{{AB}}{{AC}} = \frac{{BH}}{{AH}} = \frac{{2BN}}{{2MA}} = \frac{{BN}}{{MA}}\).
Tam giác ABN và tam giác CAM có:
\(\widehat {ABN} = \widehat {CAM}\) (cmt)
\(\frac{{AB}}{{AC}} = \frac{{BN}}{{MA}}\) (cmt)
Do đó, ∆ABN ᔕ ∆CAM (c.g.c).
Vì ∆HBA ᔕ ∆HAC (cmt). Suy ra \(\frac{{AB}}{{AC}} = \frac{{AH}}{{CH}} = \frac{{2AM}}{{2CP}} = \frac{{AM}}{{CP}}\).
Xét tam giác ACP và tam giác BAM có:
\(\widehat {ACP} = \widehat {MAB}\,\,\,\,\,\left( { = 90^\circ - \widehat {CAH}} \right)\)
\(\frac{{AB}}{{AC}} = \frac{{AM}}{{CP}}\) (cmt)
Do đó, ∆ACP ᔕ ∆BAM (c.g.c).
c)
+ Vì MN là đường trung bình trong tam giác AHB nên MN song song với AB.
Mà AB vuông góc với AC nên MN vuông góc với AC.
Trong tam giác CAN có MN vuông góc với AC nên MN là đường cao trong tam giác CAN, mà AH là đường cao trong tam giác CAN và M là giao điểm của MN và AH nên M là trực tâm của tam giác CAN. Vậy CM vuông góc với AN.
+ Vì MP là đường trung bình trong tam giác CAH nên MP song song với AC.
Mà AB vuông góc với AC nên MP vuông góc với AB.
Trong tam giác PAB có MP vuông góc với AB nên MP là đường cao trong tam giác PAB, mà AH là đường cao trong tam giác PAB và M là giao điểm của MP và AH nên M là trực tâm của tam giác PAB. Vậy AP vuông góc với BM.