Câu hỏi:
01/02/2024 91Cho tam giác ABC vuông tại A. Các tia phân giác của các góc B và C cắt nhau tại I. Gọi H, J, K lần lượt là chân đường vuông góc kẻ từ I đến AB, AC, BC. Biết KI = 5 cm, BK = 10 cm, KC = 15 cm. Diện tích tam giác ABC bằng:
A. 75 cm2;
B. 100 cm2;
C. 150 cm2;
D. 300 cm2.
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Hướng dẫn giải
Đáp án đúng là:
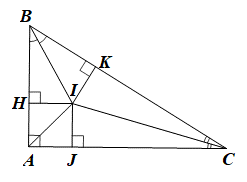
Xét DBHI và DBKI có:
\(\widehat {BHI} = \widehat {BKI} = 90^\circ \),
BI là cạnh chung;
\(\widehat {HBI} = \widehat {KBI}\) (do BI là tia phân giác của góc ABC),
Do đó DBHI = DBKI (cạnh huyền – góc nhọn).
Suy ra BH = BK = 10 cm (hai cạnh tương ứng).
Chứng minh tương tự có DIJC = DIKC (cạnh huyền – góc nhọn).
Suy ra JC = KC = 15 cm.
Vì các tia phân giác của các góc B và C cắt nhau tại I nên I là giao điểm của ba đường phân giác của tam giác ABC.
Do đó AI là tia phân giác của góc A nên \(\widehat {HAI} = \widehat {JAI} = \frac{1}{2}.90^\circ = 45^\circ .\)
Tam giác AHI vuông tại H có \(\widehat {HAI} = 45^\circ \) nên là tam giác vuông cân tại H.
Do đó IH = AH.
Chứng minh tương tự ta cũng có tam giác AJI vuông cân tại J nên AJ = IJ.
Mà I là giao điểm của ba đường phân giác của tam giác ABC nên I cách đều ba cạnh của tam giác, hay IH = IK = IJ = 5 cm.
Suy ra AH = AJ = IH = IK = IJ = 5 cm.
Ta có AB = AH + BH = 5 + 10 = 15 (cm);
AC = AJ + JC = 5 + 15 = 20 (cm).
Diện tích tam giác ABC là:
\(\frac{1}{2}\).15.20 = 150 (cm2).
Vậy ta chọn phương án C.
Hướng dẫn giải
Đáp án đúng là:

Xét DBHI và DBKI có:
\(\widehat {BHI} = \widehat {BKI} = 90^\circ \),
BI là cạnh chung;
\(\widehat {HBI} = \widehat {KBI}\) (do BI là tia phân giác của góc ABC),
Do đó DBHI = DBKI (cạnh huyền – góc nhọn).
Suy ra BH = BK = 10 cm (hai cạnh tương ứng).
Chứng minh tương tự có DIJC = DIKC (cạnh huyền – góc nhọn).
Suy ra JC = KC = 15 cm.
Vì các tia phân giác của các góc B và C cắt nhau tại I nên I là giao điểm của ba đường phân giác của tam giác ABC.
Do đó AI là tia phân giác của góc A nên \(\widehat {HAI} = \widehat {JAI} = \frac{1}{2}.90^\circ = 45^\circ .\)
Tam giác AHI vuông tại H có \(\widehat {HAI} = 45^\circ \) nên là tam giác vuông cân tại H.
Do đó IH = AH.
Chứng minh tương tự ta cũng có tam giác AJI vuông cân tại J nên AJ = IJ.
Mà I là giao điểm của ba đường phân giác của tam giác ABC nên I cách đều ba cạnh của tam giác, hay IH = IK = IJ = 5 cm.
Suy ra AH = AJ = IH = IK = IJ = 5 cm.
Ta có AB = AH + BH = 5 + 10 = 15 (cm);
AC = AJ + JC = 5 + 15 = 20 (cm).
Diện tích tam giác ABC là:
\(\frac{1}{2}\).15.20 = 150 (cm2).
Vậy ta chọn phương án C.
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Ba vị trí của khu vực A, B, C trong một trường học được mô tả như hình vẽ dưới đây.
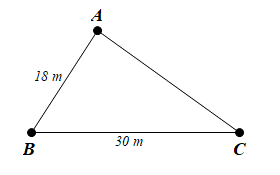
Nếu đặt ở khu vực A một thiết bị phát wifi thì cần có bán kính hoạt động là bao nhiêu để cả hai khu vực B và C đều nhận được tín hiệu?
Câu 2:
Hai nhà máy được xây dựng tại hai địa điểm A và B cùng nằm về một phía của khúc sông thẳng. Lấy điểm mốc D ở phía bên kia bờ sông là điểm đối xứng của nhà máy A qua khúc sông thẳng.
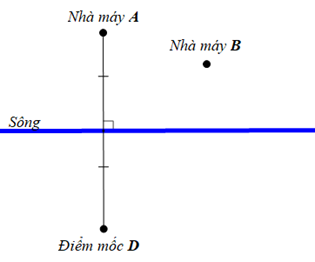
Tìm trên bờ sông một địa điểm C để xây dựng trạm bơm sao cho tổng chiều dài đường ống dẫn nước từ C đến A và đến B nhỏ nhất.
Câu 3:
Một con đường quốc lộ có vị trí với hai điểm dân cư A và B như hình vẽ dưới đây.
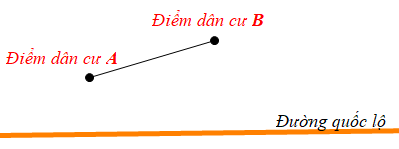
Hãy tìm trên đường quốc lộ đó một địa điểm C để xây dựng trạm y tế sao cho trạm y tế cách đều hai điểm dân cư A và B.
Câu 4:
Cho tam giác MNP có ba đường phân giác MA, NB, PC cắt nhau tại I. Vẽ IH vuông góc NP tại H. Khẳng định nào dưới đây là đúng:
Câu 5:
Cho tam giác ABC có \(\widehat A = \alpha \) là góc tù. Các đường trung trực của các cạnh AB và AC cắt nhau tại I. Tính số đo của góc BIC theo α ta được:
Câu 6:
Cho ∆ABC có AD, BE, CF là ba đường trung tuyến và trọng tâm G.
Cho các phát biểu sau:
(I) \[AD + BE + CF > \frac{3}{4}\left( {AB + BC + AC} \right)\];
(II) AD + BE + CF < AB + BC + AC.
Chọn khẳng định đúng:


