Cho tam giác ABC vuông cân tại đỉnh A. Ghép thêm vào phía ngoài tam giác đó tam giác BCD vuông cân tại đỉnh B.

Chứng minh tứ giác ABDC là một hình thang vuông (hình thang có một cạnh bên vuông góc với hai đáy).

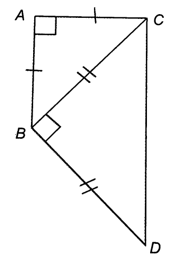
Do ∆ABC vuông cân tại đỉnh A nên  $\widehat{ABC}=\widehat{ACB};$  $\widehat{A}=90°$

Xét trong ∆ABC ta có:  $\widehat{ABC}+\widehat{ACB}+\widehat{A}=180°$ 

Nên  $\widehat{ABC}=\widehat{ACB}=\frac{180°-\widehat{A}}{2}=\frac{180°-90°}{2}=45°.$

Do ∆BCD vuông cân tại đỉnh B nên  $\widehat{BCD}=\widehat{BDC};$  $\widehat{CBD}=90°$

Xét trong ∆BCD ta có:  $\widehat{BCD}+\widehat{BDC}+\widehat{CBD}=180°$ 

Nên  $\widehat{BCD}=\widehat{BDC}=\frac{180°-\widehat{CBD}}{2}=\frac{180°-90°}{2}=45°.$

Ta có  $\widehat{ABC}=45°=\widehat{BCD}$ nên AB // CD (hai góc so le trong bằng nhau).

Vậy ABCD là một hình thang với AB, CD là hai đáy; cạnh bên của hình thang đó là AC vuông góc với đáy AB nên hình thang đó là hình thang vuông.