Cho hình thang cân ABCD với hai đáy AB và CD, đường chéo AC vuông góc với cạnh bên AD, tia CA là tia phân giác của góc C.

Tính chu vi của hình thang đó biết rằng AD = 2 cm.

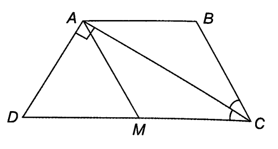
Do CA là tia phân giác của  $\widehat{C}$ nên  $\widehat{BCA}=\widehat{ACD}$

Mà ABCD là hình thang cân nên AB // CD, suy ra  $\widehat{BAC}=\widehat{ACD}$ (hai góc so le trong)

Do đó,  $\widehat{BAC}=\widehat{BCA}$, suy ra ∆ABC cân tại B.

Đặt  $\widehat{BAC}=\alpha$ thì  $\widehat{C}=2\alpha$.

Vì ABCD là hình thang cân nên  $\widehat{D}=\widehat{C}=2\alpha .$

Tam giác ADC vuông tại A nên  $\widehat{ADC}+\widehat{ACD}=2\alpha +\alpha =90°,$ suy ra  $\alpha =30°,\widehat{D}=60°.$

Lấy điểm M thuộc cạnh huyền DC sao cho DM = AD, mà  $\widehat{D}=60°$ thì AMD là tam giác đều, nên  $\widehat{MAD}=60°$

Khi đó  $\widehat{MAC}=\widehat{CAD}-\widehat{MAD}=90°-60°=30°$

Suy ra  $\widehat{ACM}=\widehat{CAM}=30°$ nên tam giác MAC cân tại M

Do đó AM = MC, mà AM = DM = AD

Nên AM = DM = AD = MC hay DC = 2AD.

Vậy AB = BC = AD, DC = 2AD nên chu vi hình thang bằng

AB + BC + CD + AD = 5AD = 5.2 = 10 cm.