Câu hỏi:
05/04/2024 35
Cho tam giác ABC nhọn, các đường cao AD, BE, CF đồng quy tại H. Gọi M, N, P, Q lần lượt là hình chiếu của D trên AB, BE, CF, AC. Khẳng định nào sau đây sai?
Cho tam giác ABC nhọn, các đường cao AD, BE, CF đồng quy tại H. Gọi M, N, P, Q lần lượt là hình chiếu của D trên AB, BE, CF, AC. Khẳng định nào sau đây sai?
A. EF // MC;
B. MN // EF;
C. PQ // EF;
D. M, N, P, Q thẳng hàng.
Trả lời:
Giải bởi Vietjack
Đáp án đúng là: A
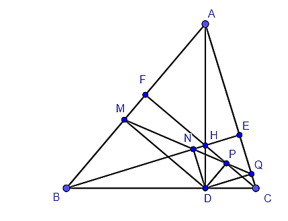
Ta có QD ⊥ AC, HE ⊥ AC (H ∈ BE) nên HE // QD hay BE // QD (H ∈ BE).
Xét tam giác ADQ có HE // DQ nên theo định lí Thalès ta có: (1).
Có HF ⊥ AB (H ∈ CF), DM ⊥ AB nên HF // DM hay CF // DM.
Xét tam giác AMD có HF // DM nên theo định lí Thalès ta có: (2).
Từ (1) và (2) suy ra .
Trong tam giác AMQ có nên EF // MQ (định lí Thaslès đảo) (*).
Xét tam giác BFC có CF // DM nên theo định lí Thalès ta có: (3).
Có DN ⊥ BE, BE ⊥ EC (E ∈ AC) nên DN // CE.
Xét tam giác BEC có DN // CE nên theo định lí Thalès ta có: (4).
Từ (3) và (4) suy ra .
Trong tam giác BEF có nên MN // EF (định lí Thaslès đảo) (**).
Xét tam giác BEC có QD // BE nên theo định lí Thalès ta có: (5).
Có DP ⊥ CF, BF ⊥ CF (F ∈ AB) nên DP // BF.
Xét tam giác BFC có DP // BF nên theo định lí Thalès ta có: (6).
Từ (5) và (6) suy ra .
Trong tam giác CEF có nên PQ // EF (định lí Thaslès đảo)(***)
Từ (*), (**), (***) suy ra M, N, P, Q thẳng hàng.
Vậy A sai.
Đáp án đúng là: A
Ta có QD ⊥ AC, HE ⊥ AC (H ∈ BE) nên HE // QD hay BE // QD (H ∈ BE).
Xét tam giác ADQ có HE // DQ nên theo định lí Thalès ta có: (1).
Có HF ⊥ AB (H ∈ CF), DM ⊥ AB nên HF // DM hay CF // DM.
Xét tam giác AMD có HF // DM nên theo định lí Thalès ta có: (2).
Từ (1) và (2) suy ra .
Trong tam giác AMQ có nên EF // MQ (định lí Thaslès đảo) (*).
Xét tam giác BFC có CF // DM nên theo định lí Thalès ta có: (3).
Có DN ⊥ BE, BE ⊥ EC (E ∈ AC) nên DN // CE.
Xét tam giác BEC có DN // CE nên theo định lí Thalès ta có: (4).
Từ (3) và (4) suy ra .
Trong tam giác BEF có nên MN // EF (định lí Thaslès đảo) (**).
Xét tam giác BEC có QD // BE nên theo định lí Thalès ta có: (5).
Có DP ⊥ CF, BF ⊥ CF (F ∈ AB) nên DP // BF.
Xét tam giác BFC có DP // BF nên theo định lí Thalès ta có: (6).
Từ (5) và (6) suy ra .
Trong tam giác CEF có nên PQ // EF (định lí Thaslès đảo)(***)
Từ (*), (**), (***) suy ra M, N, P, Q thẳng hàng.
Vậy A sai.
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
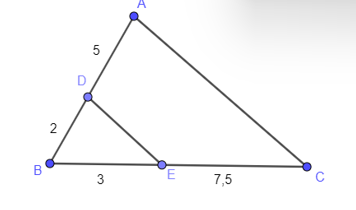
Cho hình bên, biết AB = 9 cm, AC = 12 cm, IB = 6 cm, KC = 8 cm. Kết luận nào sau đây là đúng?
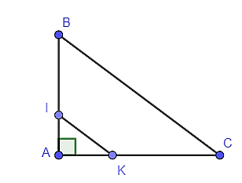
Cho hình bên, biết AB = 9 cm, AC = 12 cm, IB = 6 cm, KC = 8 cm. Kết luận nào sau đây là đúng?
Câu 4:
Cho tam giác ABC, I và K là hai điểm bất kì trên cạnh AB và AC. Từ I kẻ IM // BK (M ∈ AC), từ K kẻ KN // CI (N ∈ AB). Khi đó MN …… BC. Từ thích hợp điền vào chỗ chấm là:
Cho tam giác ABC, I và K là hai điểm bất kì trên cạnh AB và AC. Từ I kẻ IM // BK (M ∈ AC), từ K kẻ KN // CI (N ∈ AB). Khi đó MN …… BC. Từ thích hợp điền vào chỗ chấm là:
Câu 6:
Cho tam giác ABC. Điểm O nằm trong tam giác. Lấy điểm D trên AO, từ D kẻ DE // AB (E ∈ OB) và DF // AC (F ∈ OC). Khẳng định nào sau đây là sai?
Cho tam giác ABC. Điểm O nằm trong tam giác. Lấy điểm D trên AO, từ D kẻ DE // AB (E ∈ OB) và DF // AC (F ∈ OC). Khẳng định nào sau đây là sai?
Câu 7:
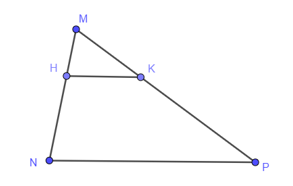
Cho tứ giác MNPQ, gọi K, L lần lượt là trọng tâm của tam giác MNP và NPQ. Khi đó KL song song với đường thẳng nào dưới đây?
Cho tứ giác MNPQ, gọi K, L lần lượt là trọng tâm của tam giác MNP và NPQ. Khi đó KL song song với đường thẳng nào dưới đây?
Câu 8:
Cho tam giác ABC có điểm M trên cạnh BC sao cho BC = 4CM. Trên cạnh AC lấy điểm N sao cho . Khẳng định nào sau đây là đúng khi nói về mối quan hệ giữa hai đường thẳng AB và MN.
Cho tam giác ABC có điểm M trên cạnh BC sao cho BC = 4CM. Trên cạnh AC lấy điểm N sao cho . Khẳng định nào sau đây là đúng khi nói về mối quan hệ giữa hai đường thẳng AB và MN.
Câu 9:
Cho tam giác ABC vuông tại A, đường cao AH. Từ điểm D nằm giữa H và C, vẽ DE ⊥ DC (E ∈ AC), DK ⊥ AC (K ∈ AC). Khi đó BE song song với
Cho tam giác ABC vuông tại A, đường cao AH. Từ điểm D nằm giữa H và C, vẽ DE ⊥ DC (E ∈ AC), DK ⊥ AC (K ∈ AC). Khi đó BE song song với
