Câu hỏi:
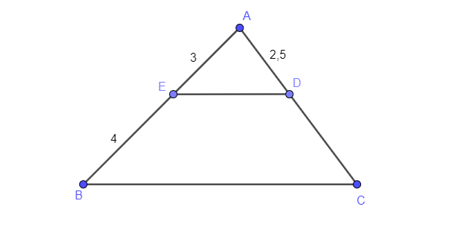
05/04/2024 57Cho tam giác ABC, DE là đường trung bình của tam giác (hình bên dưới). Khi đó ΔAED ᔕ ΔABC theo tỉ số đồng dạng k bằng:
A. ;
A. ;
B. 2;
B. 2;
C. 1
D. 0.
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Hướng dẫn giải:
Đáp án đúng là: A
Vì DE là đường trung bình của tam giác ABC nên ta có:
+ (D là trung điểm AC).
+ (E là trung điểm AB).
+ và DE // BC (tính chất đường trung bình).
DE // BC suy ra (các góc đồng vị).
Suy ra ΔAED ᔕ ΔABC với tỉ số k =  .
.
Hướng dẫn giải:
Đáp án đúng là: A
Vì DE là đường trung bình của tam giác ABC nên ta có:
+ (D là trung điểm AC).
+ (E là trung điểm AB).
+ và DE // BC (tính chất đường trung bình).
DE // BC suy ra (các góc đồng vị).
Suy ra ΔAED ᔕ ΔABC với tỉ số k = ![]() .
.
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 2:
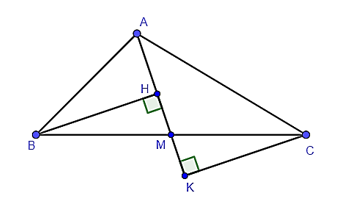
Cho tam giác ABC có AM là đường trung tuyến. Kẻ BH và CK lần lượt vuông góc với AM (hình bên dưới). Khi đó tam giác MBH đồng dạng với tam giác nào dưới đây?
Câu 3:
Cho ΔABC ᔕ ΔMNQ với tỉ số đồng dạng k = 3, biết AC = 12 cm. Độ dài cạnh QM bằng:
Cho ΔABC ᔕ ΔMNQ với tỉ số đồng dạng k = 3, biết AC = 12 cm. Độ dài cạnh QM bằng:
Câu 4:
Cho ΔABC ᔕ ΔADE với tỉ số đồng dạng k, biết DE = 4, BC = 12. Tỉ số đồng dạng k bằng
Cho ΔABC ᔕ ΔADE với tỉ số đồng dạng k, biết DE = 4, BC = 12. Tỉ số đồng dạng k bằng
Câu 6:
ΔABC ᔕ ΔDEF với tỉ số đồng dạng là . Khi đó ΔDEF ᔕ ΔABC theo tỉ số đồng dạng k bằng bao nhiêu?
ΔABC ᔕ ΔDEF với tỉ số đồng dạng là . Khi đó ΔDEF ᔕ ΔABC theo tỉ số đồng dạng k bằng bao nhiêu?
Câu 8:
Cho ΔABC ᔕ ΔDEF với tỉ số đồng dạng k1 = 2, ΔDEF ᔕ ΔMNQ với tỉ số đồng dạng k2 = 3. Khẳng định nào sau đây là đúng?
Cho ΔABC ᔕ ΔDEF với tỉ số đồng dạng k1 = 2, ΔDEF ᔕ ΔMNQ với tỉ số đồng dạng k2 = 3. Khẳng định nào sau đây là đúng?