Câu hỏi:
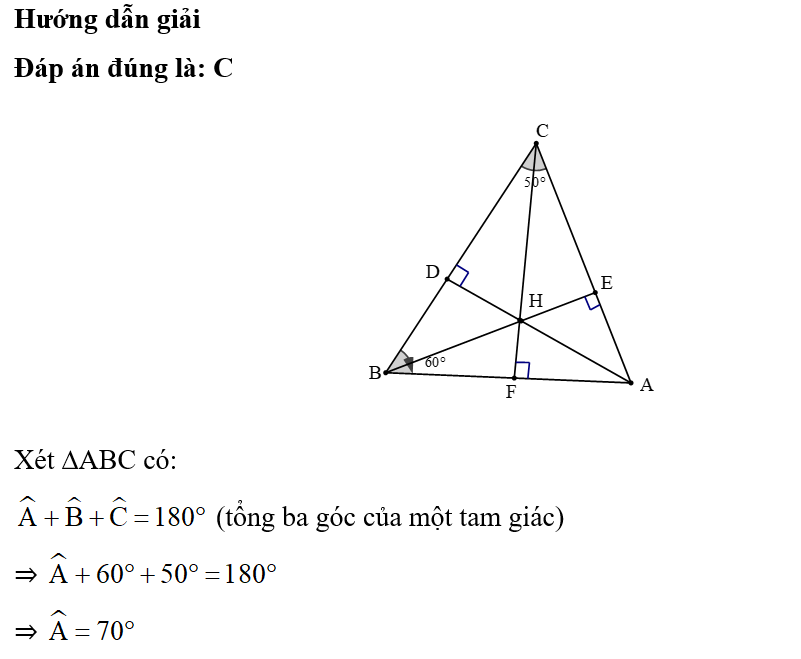
31/01/2024 62Cho ∆ABC có ˆB=60°; ˆC=50°. Ba đường cao AD, BE, CF cắt nhau tại H. Số đo ^BHC là
A. 98°;
A. 98°;
B. 108°;
B. 108°;
C. 110°;
Đáp án chính xác
D. 70°.
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack

CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 2:
Cho tam giác nhọn MNP có hai đường cao NE và PF cắt nhau tại H. Biết NE = PF. Khẳng định đúng là
Cho tam giác nhọn MNP có hai đường cao NE và PF cắt nhau tại H. Biết NE = PF. Khẳng định đúng là
Xem đáp án »
31/01/2024
74
Câu 3:
Cho ∆ABC cân tại A có trực tâm I. Biết ^BIC=120°. Số đo các góc của ∆ABC là
Cho ∆ABC cân tại A có trực tâm I. Biết ^BIC=120°. Số đo các góc của ∆ABC là
Xem đáp án »
31/01/2024
69
Câu 4:
Cho ∆ABC nhọn, hai đường cao BD và CE gặp nhau tại H. Vẽ điểm K sao cho AB là trung trực của HK. So sánh đúng là
Cho ∆ABC nhọn, hai đường cao BD và CE gặp nhau tại H. Vẽ điểm K sao cho AB là trung trực của HK. So sánh đúng là
Xem đáp án »
31/01/2024
68
Câu 5:
Cho ∆ABC cân tại B có chu vi là 60cm, đường cao BH. Biết chu vi ∆ABH là 40cm. Độ dài BH là
Cho ∆ABC cân tại B có chu vi là 60cm, đường cao BH. Biết chu vi ∆ABH là 40cm. Độ dài BH là
Xem đáp án »
31/01/2024
64
Câu 6:
Cho ∆ABC có diện tích là 180 cm2 và cạnh BC = 20 cm. Độ dài đường cao ứng với cạnh BC là
Xem đáp án »
31/01/2024
63



