Câu hỏi:
25/01/2024 50
Cho ∆ABC có , . Gọi AD là tia nằm giữa hai tia AB và AC sao cho . Số đo của bằng:
Cho ∆ABC có , . Gọi AD là tia nằm giữa hai tia AB và AC sao cho . Số đo của bằng:
A. 10°;
A. 10°;
B. 30°;
B. 30°;
C. 45°;
D. 60°.
Đáp án chính xác
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Hướng dẫn giải
Đáp án đúng là: D
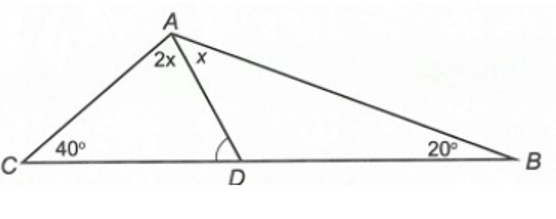
∆ABC có: (định lí tổng ba góc trong một tam giác)
Suy ra .
Gọi (x > 0).
Suy ra .
Ta có .
Suy ra x + 2x = 120°.
Khi đó 3x = 120°.
Vì vậy x = 120° : 3 = 40°.
Suy ra .
∆ACD có: (định lí tổng ba góc trong một tam giác)
Suy ra .
Vậy ta chọn phương án D.
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Cho ∆ABC vuông tại A. Kẻ AH vuông góc với BC (H ∈ BC). Các tia phân giác của và cắt nhau tại I. Khi đó ∆AIB là:
Xem đáp án »
25/01/2024
59
Câu 2:
Cho ∆MNP. Các đường phân giác trong các , cắt nhau tại I. Kết luận nào sau đây đúng?
Cho ∆MNP. Các đường phân giác trong các , cắt nhau tại I. Kết luận nào sau đây đúng?
Xem đáp án »
25/01/2024
50


