Câu hỏi:
01/02/2024 56Cho tam giác ABC có AB < AC. Trên AC lấy điểm D sao cho AB = CD. O là giao điểm của các đường trung trực của BD và AC. Phát biểu nào sau đây là đúng?
A. ΔABO = ∆COD;
B. ΔAOB = ∆COD;
C. ΔABO = ∆CDO;
D. ΔBOA = ∆COD.
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Hướng dẫn giải
Đáp án đúng là: B
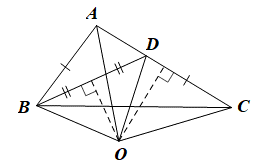
Vì O thuộc đường trung trực của AC nên OA = OC;
Vì O thuộc đường trung trực của BD nên OB = OD.
Xét ΔAOB và ΔCOD có
OA = OC (chứng minh trên),
OB = OD (chứng minh trên),
AB = CD (giả thiết)
Do đó ΔAOB = ΔCOD (c.c.c).
Vậy ta chọn phương án B.
Hướng dẫn giải
Đáp án đúng là: B

Vì O thuộc đường trung trực của AC nên OA = OC;
Vì O thuộc đường trung trực của BD nên OB = OD.
Xét ΔAOB và ΔCOD có
OA = OC (chứng minh trên),
OB = OD (chứng minh trên),
AB = CD (giả thiết)
Do đó ΔAOB = ΔCOD (c.c.c).
Vậy ta chọn phương án B.
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Cho góc xOy có số đo là 50º, điểm A nằm trong góc xOy. Vẽ điểm M sao cho Ox là trung trực của AM, vẽ điểm N sao cho Oy là trung trực của AN. Số đo góc MON là:
Câu 2:
Cho tam giác ABC nhọn, đường cao AH. Lấy điểm D sao cho AB là trung trực của HD. Lấy điểm E sao cho AC là trung trực của HE. Gọi M là giao điểm của DE và AB, gọi N là giao điểm của DE và AC. Khẳng định nào sau đây là đúng?
Câu 3:
Cho góc nhọn \(\widehat {xOy}\), trên tia Ox lấy điểm A, trên tia Oy lấy điểm B sao cho OA = OB. Đường trung trực của OA và đường trung trực của OB cắt nhau tại I.
Cho các khẳng định sau:
(I) OI là tia phân giác của \(\widehat {xOy}\);
(II) OI là đường trung trực của đoạn AB.
Chọn khẳng định đúng:
Câu 4:
Cho tam giác ABC có AB < AC. Trên AC lấy điểm D sao cho AB = CD. O là giao điểm của các đường trung trực của BD và AC. Phát biểu nào sau đây là đúng?
Câu 5:
Cho tam giác ABC có góc A là góc tù. Gọi M, N lần lượt là trung điểm của AB và AC. Vẽ đường trung trực của các cạnh AB, AC cắt BC lần lượt tại D và E. Biết BD = 3 cm, DE = 2 cm, EC = 4 cm. Chu vi tam giác ADE bằng:
Câu 6:
Cho tam giác ABC có M là trung điểm của BC. Các đường trung trực của AB và AC cắt nhau tại O. Số đo góc OMC là:


