Câu hỏi:
31/01/2024 76
Cho ∆ABC cân tại A. Trên 2 cạnh AB và AC lấy hai điểm M và N sao cho AM = AN. So sánh BN với BC + MN đúng là
Cho ∆ABC cân tại A. Trên 2 cạnh AB và AC lấy hai điểm M và N sao cho AM = AN. So sánh BN với BC + MN đúng là
A. ;
A. ;
B. ;
B. ;
C. ;
D. Không đủ dữ kiện để so sánh.
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Hướng dẫn giải
Đáp án đúng là: A
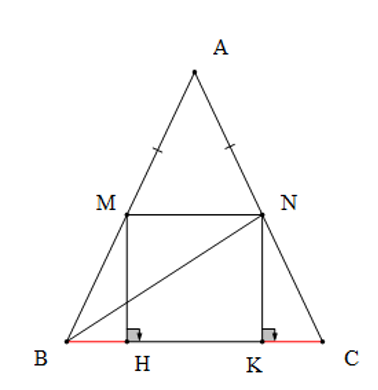
∆ABC cân tại A nên AB = AC và (tính chất)
Mà AM = AN (giả thiết) suy ra BM = CN
Xét hai tam giác vuông MBH và NCK có:
BM = CN
Suy ra ∆MBH = ∆NCK (cạnh huyền – góc nhọn)
Do đó: BH = CK và MH = NK
Có AM = AN (giả thiết) suy ra ∆AMN cân tại A
⇒ (tính chất)
Mà (tổng ba góc của một tam giác)
Suy ra (1)
Có mà (tổng ba góc của một tam giác)
Suy ra (1)
Từ (1) và (2) suy ra mà hai góc đồng vị nên MN // BC.
Mà BC ⊥ MH nên MN ⊥ MH
Xét hai tam giác vuông HMN và NKH có
MH = NK (chứng minh trên)
NH là cạnh chung
Suy ra ∆HMN = ∆NKH (cạnh huyền – cạnh góc vuông)
Do đó MN = HK
Mặt khác: BN > BK (quan hệ đường vuông góc – đường xiên)
Suy ra: 2BN > 2BK = 2(BH + HK) = 2BH + 2HK = BH + KC + MN + HK = BC + MN
Do đó: .
Hướng dẫn giải
Đáp án đúng là: A

∆ABC cân tại A nên AB = AC và (tính chất)
Mà AM = AN (giả thiết) suy ra BM = CN
Xét hai tam giác vuông MBH và NCK có:
BM = CN
Suy ra ∆MBH = ∆NCK (cạnh huyền – góc nhọn)
Do đó: BH = CK và MH = NK
Có AM = AN (giả thiết) suy ra ∆AMN cân tại A
⇒ (tính chất)
Mà (tổng ba góc của một tam giác)
Suy ra (1)
Có mà (tổng ba góc của một tam giác)
Suy ra (1)
Từ (1) và (2) suy ra mà hai góc đồng vị nên MN // BC.
Mà BC ⊥ MH nên MN ⊥ MH
Xét hai tam giác vuông HMN và NKH có
MH = NK (chứng minh trên)
NH là cạnh chung
Suy ra ∆HMN = ∆NKH (cạnh huyền – cạnh góc vuông)
Do đó MN = HK
Mặt khác: BN > BK (quan hệ đường vuông góc – đường xiên)
Suy ra: 2BN > 2BK = 2(BH + HK) = 2BH + 2HK = BH + KC + MN + HK = BC + MN
Do đó: .
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Cho ∆ABC có . M là điểm nằm giữa B và C. Vẽ điểm E sao cho AB là trung trực của ME, Điểm F sao cho AC là trung trực của MF. Khẳng định nào dưới đây sai?
Cho ∆ABC có . M là điểm nằm giữa B và C. Vẽ điểm E sao cho AB là trung trực của ME, Điểm F sao cho AC là trung trực của MF. Khẳng định nào dưới đây sai?
Câu 2:
Cho ∆ABC cân tại A, trên các cạnh AB, AC lần lượt lấy hai điểm P và Q sao cho AP = AQ. Hai đoạn thẳng CP và BQ cắt nhau tại O. OH và OK lần lượt là khoảng cách từ O đến AB và AC. Khẳng định nào dưới đây sai?
Cho ∆ABC cân tại A, trên các cạnh AB, AC lần lượt lấy hai điểm P và Q sao cho AP = AQ. Hai đoạn thẳng CP và BQ cắt nhau tại O. OH và OK lần lượt là khoảng cách từ O đến AB và AC. Khẳng định nào dưới đây sai?
Câu 3:
Cho ∆ABC nhọn có đường cao BD và CE. Trên tia đối của tia BD lấy điểm I sao cho BI = AC. Trên tia đối của tia CE lấy điểm K sao cho CK = AB. Chọn câu đúng nhất.
Cho ∆ABC nhọn có đường cao BD và CE. Trên tia đối của tia BD lấy điểm I sao cho BI = AC. Trên tia đối của tia CE lấy điểm K sao cho CK = AB. Chọn câu đúng nhất.
Câu 4:
Cho tam giác ABC có AB = AC . Trên cạnh AB và AC lấy các điểm D, E sao cho AD = AE. Gọi K là giao điểm của BE và CD. Chọn câu sai.
Cho tam giác ABC có AB = AC . Trên cạnh AB và AC lấy các điểm D, E sao cho AD = AE. Gọi K là giao điểm của BE và CD. Chọn câu sai.
Câu 5:
Cho ∆ABC (AB < AC). Đường trung trực của BC cắt BC tại E và cắt AC tại F. Lấy điểm M bất kỳ trên đường thẳng d (M ≠ F). So sánh chu vi ∆AFB và chu vi ∆AMB đúng là
Cho ∆ABC (AB < AC). Đường trung trực của BC cắt BC tại E và cắt AC tại F. Lấy điểm M bất kỳ trên đường thẳng d (M ≠ F). So sánh chu vi ∆AFB và chu vi ∆AMB đúng là
Câu 6:
Cho tam giác ABC vuông tại A, tia phân giác góc B cắt AC tại D. Biết . Số đo góc ACB là
Cho tam giác ABC vuông tại A, tia phân giác góc B cắt AC tại D. Biết . Số đo góc ACB là
Câu 7:
Cho khác góc bẹt, lấy điểm A thuộc tia Ox, điểm B thuộc tia Oy sao cho OA = OB. Lấy M là trung điểm của AB. Khẳng định nào dưới đây đúng?
Cho khác góc bẹt, lấy điểm A thuộc tia Ox, điểm B thuộc tia Oy sao cho OA = OB. Lấy M là trung điểm của AB. Khẳng định nào dưới đây đúng?
Câu 8:
Cho hình vẽ dưới đây, biết AB vuông góc với BC, AD vuông góc với CD và cạnh AB = AD. Khẳng định sai là
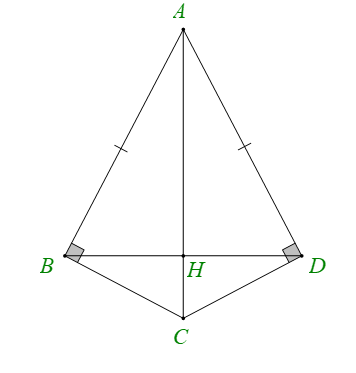
Cho hình vẽ dưới đây, biết AB vuông góc với BC, AD vuông góc với CD và cạnh AB = AD. Khẳng định sai là

Câu 9:
Cho ∆ABC cân tại A. Tia phân giác của góc B và góc C cắt cạnh AC, AB lần lượt ở D và E. Đoạn thẳng có độ dài bằng đoạn thẳng BE là
Cho ∆ABC cân tại A. Tia phân giác của góc B và góc C cắt cạnh AC, AB lần lượt ở D và E. Đoạn thẳng có độ dài bằng đoạn thẳng BE là


