Bài 1 trang 65 SBT Toán 7 Tập 2: Cho tam giác ABC cân tại A. Gọi G là trọng tâm của tam giác và gọi I là giao điểm của các đường phân giác của tam giác. Chứng minh ba điểm A, I, G thẳng hàng.
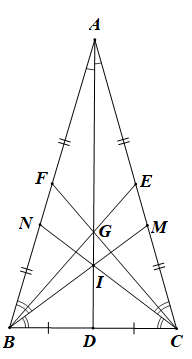
Vẽ phân giác AD của tam giác ABC.
Xét ABD và ACD có:
AB = AC (do ABC cân tại A),
(do AD là phân giác của ),
AD là cạnh chung.
Do đó ABD = ACD (c.g.c)
Suy ra DB = DC.
Khi đó AD vừa là đường phân giác vừa là đường trung tuyến của tam giác ABC.
Mà G là trọng tâm của tam giác và I là giao điểm của các đường phân giác của tam giác ABC.
Suy ra hai điểm I và G đều thuộc AD.
Khi đó ba điểm A, I, G thẳng hàng.
Vậy ba điểm A, I, G thẳng hàng.
Xem thêm lời giải sách bài tập Toán lớp 7 Chân trời sáng tạo hay, chi tiết khác:
Bài 7: Tính chất ba đường trung tuyến của tam giác
Bài 8: Tính chất ba đường cao của tam giác
Bài 9: Tính chất ba đường phân giác của tam giác