Câu hỏi:
31/01/2024 69
Cho tam giác ABC cân tại A có AH là đường phân giác của góc BAC (H ∈ BC). Khẳng định sai là
Cho tam giác ABC cân tại A có AH là đường phân giác của góc BAC (H ∈ BC). Khẳng định sai là
A. AH ⊥ BC;
A. AH ⊥ BC;
B. AH là đường trung trực của đoạn thẳng BC;
B. AH là đường trung trực của đoạn thẳng BC;
C. HB = HC;
D. HA = HB.
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Hướng dẫn giải
Đáp án đúng là: D
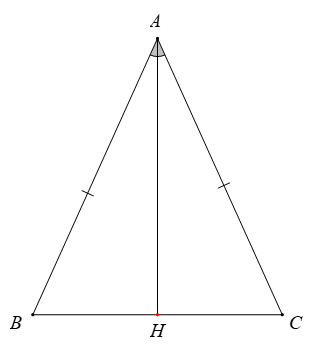
Xét tam giác ABH và tam giác ACH có:
AB = AC (∆ABC cân tại A)
(AH là đường phân giác của )
AH là cạnh chung
Do đó, ∆ABH = ∆ACH (c.g.c)
⇒ HB = HC (hai cạnh tương ứng) (1)
Và (hai góc tương ứng)
Mà (hai góc kề bù)
⇒⇒ AH ⊥ BC (2)
Từ (1) và (2) ⇒AH là đường trung trực của đoạn thẳng BC.
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Cho ∆ABC (AB < AC). Đường trung trực của BC cắt BC tại E và cắt AC tại F. Lấy điểm M bất kỳ trên đường thẳng d (M ≠ F). So sánh chu vi ∆AFB và chu vi ∆AMB đúng là
Cho ∆ABC (AB < AC). Đường trung trực của BC cắt BC tại E và cắt AC tại F. Lấy điểm M bất kỳ trên đường thẳng d (M ≠ F). So sánh chu vi ∆AFB và chu vi ∆AMB đúng là
Câu 2:
Cho M, N là hai điểm phân biệt nằm trên đường trung trực của cạnh AB sao cho AM = BN. O là giao điểm của MN và AB. Khẳng định sai là
Cho M, N là hai điểm phân biệt nằm trên đường trung trực của cạnh AB sao cho AM = BN. O là giao điểm của MN và AB. Khẳng định sai là


