Bài 4 trang 72 SBT Toán 8 Tập 1: Cho tam giác ABC cân tại A , các đường cao BD và CE cắt nhau tại H. Tia phân giác của góc ABD cắt EC và AC lần lượt tại M và P. Tia phân giác của góc ACE cắt DB và AB lần lượt tại Q và N. Chứng minh rằng:
a) ;
b) BH = CH;
c) Tam giác BOC vuông cân;
d) MNPQ là hình vuông.
Chú ý: Câu c bổ sung dữ kiện “O là giao điểm của BP và CN”.
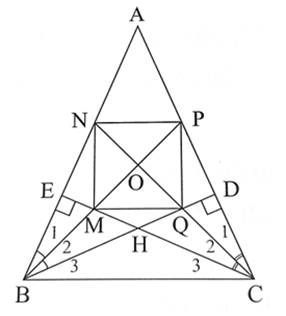
a) Ta có:
∆ABD vuông tại D (do BD là đường cao ∆ABC), suy ra ;
∆AEC vuông tại E (do CE là đường cao ∆ABC), suy ra .
Do đó .
b) ∆ABC cân tại A nên .
Mà (theo câu a).
Suy ra hay .
Do đó ∆HBC cân tại H nên BH = CH.
c) Ta có (do BP là tia phân giác ) và (do CN là tia phân giác )
Mà , suy ra .
∆OBC có , nên hay .
Suy ra ∆OBC cân tại O (1)
Mặt khác, vì (cùng bằng ) nên ta có
.
Mà
Suy ra .
Do đó tam giác OBC vuông tại O (2)
Từ (1) và (2) suy ra ∆OBC vuông cân tại O.
d) ∆OBC cân tại O nên OB = OC. (3)
Xét ∆BMH và ∆CQH có:
(theo câu b);
BH = CH (do ∆HBC cân tại H);
(hai góc đối đỉnh).
Do đó ∆BMH= ∆CQH (g.c.g).
Suy ra BM = CQ. (4)
Từ (3) và (4) suy ra OB ‒ BM = OC ‒ CQ hay OM = OQ. (5)
Mà ∆BNQ có BO là đường cao cũng đường phân giác nên ∆BNQ cân tại B.
Suy ra BO cũng là đường trung tuyến, nên O là trung điểm của QN hay ON = OQ.(6)
Chứng minh tương tự, ta được OP = OM. (7)
Từ (5), (6), (7) suy ra OM = ON = OQ = OP.
Khi đó ON + OQ = OM + OP hay NQ = MP.
Xét tứ giác MNPQ có: OM = OP và OQ = ON nên tứ giác MNPQ là hình bình hành.
Mà NQ = MP nên MNPQ là hình chữ nhật.
Ta lại có MP ⊥ NP tại O nên MNPQ là hình vuông.
Xem thêm các bài giải sách bài tập Toán 8 Chân trời sáng tạo hay, chi tiết khác:
Bài 3: Hình thang – Hình thang cân
Bài 4: Hình bình hành – Hình thoi
Bài 5: Hình chữ nhật – Hình vuông
Bài tập cuối chương 3 trang 72