Cho tam giác ABC, các đường trung tuyến BD và CE cắt nhau tại G. Gọi I, K lần lượt là trung điểm của GB, GC

Bài 4.25 trang 89 Toán 8 Tập 1: Cho tam giác ABC, các đường trung tuyến BD và CE cắt nhau tại G. Gọi I, K lần lượt là trung điểm của GB, GC. Chứng minh tứ giác EDKI là hình bình hành.

Trả lời

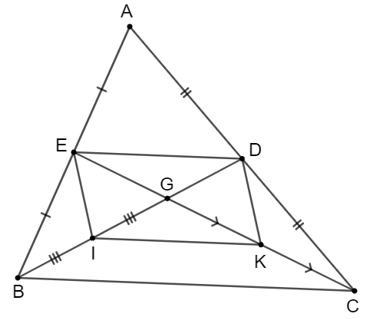
Vì BD và CE là đường trung tuyến nên E, D lần lượt là trung điểm của AB, AC.

Suy ra DE là đường trung bình của tam giác ABC.

Khi đó, DE // BC và $DE=\frac{1}{2}BC$         (1)

Vì I, K lần lượt là trung điểm của GB, GC nên IK là đường trung bình của tam giác GBC suy ra IK // BC và $IK=\frac{1}{2}BC$ (2)

Từ (1) và (2) suy ra DE // IK và $DE=IK=\frac{1}{2}BC$.

Tứ giác EDKI có DE // IK và DE = IK nên tứ giác EDKI là hình bình hành (đpcm).

Xem thêm các bài giải SGK Toán 8 Kết nối tri thức hay, chi tiết khác: