Cho một tam giác đều ABC cạnh a. Tam giác A1B1C1 có các đỉnh là trung điểm các cạnh của tam giác ABC
2k
16/05/2023
Bài 7 trang 80 Toán 11 Tập 1: Cho một tam giác đều ABC cạnh a. Tam giác A1B1C1 có các đỉnh là trung điểm các cạnh của tam giác ABC, tam giác A2B2C2 có các đỉnh là trung điểm các cạnh của tam giác A2B2C2, ..., Tam giác An+1Bn+1Cn+1 có các đỉnh là trung điểm các cạnh của tam giác AnBnCn, ... Gọi p1, p2, ..., pn, ... và S1, S2, ..., Sn, ... theo thứ tự là chu vi và diện tích của tam giác A1B1C1, A2B2C2, ..., AnBnCn, ...
a) Tìm giới hạn của dãy số (pn) và (Sn).
b) Tính các tổng p1 + p2 + ... + pn + ... và S1 + S2 + ... + Sn + ... .
Trả lời
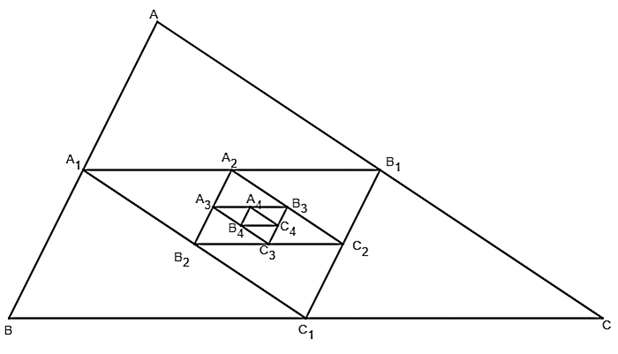
a)
+) (pn) là dãy số chu vi của các tam giác theo thứ tự ABC, A1B1C1, ...
Ta có: p1 = p∆ABC = a + a + a = 3a;
p2 = pΔA1B1C1=a2+a2+a2=12.(3a)=12.p1;
p3 = pΔA2B2C2=a4+a4+a4=(12)2.(3a)=(12)2.p1; ...; pΔAnBnCn=(12)n−1.p1; ...
Suy ra:
limn→∞pn=limn→∞((12)n−1.(3a))=limn→∞(12)n−1.limn→∞(3a)=0.3a=0.
+) (Sn) là dãy số chu vi của các tam giác theo thứ tự ABC, A1B1C1, ...
Gọi h là chiều cao của tam giác ABC và h = a√32.
Ta có: S1 = S∆ABC = 12ah; S2 = SΔA1B1C1=12.a2.h2=14.(12ah)=14.S1;
S3 = SΔA2B2C2=12.a4.h4=(14)2.(12ah)=(14)2.S1; ...; SΔAnBnCn=(12)n−1.S1; ...
Suy ra limn→∞Sn=limn→∞((14)n−1.S1)=limn→∞(14)n−1.limn→∞(12ah)=0.12ah=0.
b) +) Ta có (pn) là một cấp số nhân lùi vô hạn với số hạng đầu p1 = 3a và công bội q = 12thỏa mãn |q| < 1 có tổng:
Pn=p1+p2+...+pn+...=3a1−12=6a.
+) Ta cũng có (Sn) là một cấp số nhân lùi vô hạn với số hạng đầu S1 = 12ah và công bội q = 14 thỏa mãn |q| < 1 có tổng:
Sn=S1+S2+...+Sn+...=12ah1−14=23ah.
Xem thêm lời giải bài tập Toán lớp 11 Cánh diều hay, chi tiết khác:
Bài 2: Giới hạn của hàm số
Bài 3: Hàm số liên tục
Bài tập cuối chương 3

