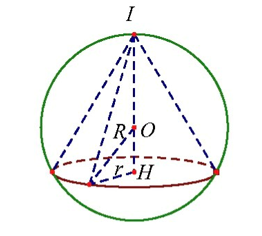
Cho mặt cầu S (O;4) cố định. Hình nón (N) gọi là nội tiếp mặt cầu S(O;4) nếu hình nón
56
01/05/2024
Cho mặt cầu S (O;4) cố định. Hình nón (N) gọi là nội tiếp mặt cầu S(O;4) nếu hình nón (N) có đường tròn đáy và đỉnh thuộc mặt cầu S( O;4). Tính bán kính đáy r của (N) để khối nón (N) có thể tích lớn nhất ?
A. r=3√2.
B. r=4√23.
C. r=2√2.
D. r=8√23.
Trả lời
Chọn D
Gọi I là đỉnh và H là tâm đáy của hình nón (N) . Do IH⊥mp(H);OH⊥mp(H)
⇒I,O,H thẳng hàng.
Dễ thấy để (N) có thể tích lớn nhất thì chỉ cần O nằm giữa đoạn IH.
Gọi đường cao của hình nón là: h=IH=OI+OH=R+OH,R≤h≤2R.
Suy ra r2=R2−(h−R)2.
Thể tích khối nón là: V=13.πr2h=13.πh[R2−(h−R)2]=13.π(−h3+2Rh2)=f(h).
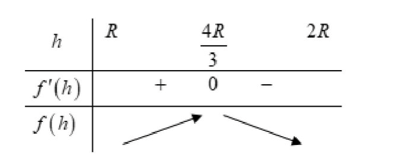
Ta có f', cho
Bảng biến thiên:
Vậy max khi