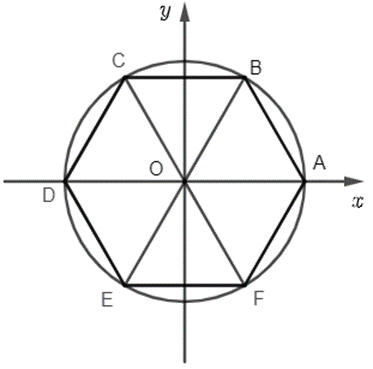
Cho lục giác đều ABCDEF nội tiếp trong đường tròn lượng giác (thứ tự đi từ A đến các đỉnh theo chiều dương). Khi đó, số đo của góc lượng giác (OA, OC) bằng:

A. \(\frac{{2\pi }}{3} + k2\pi \).

B. \( - \frac{{2\pi }}{3} + k2\pi \).

C. \(\frac{\pi }{3} + k2\pi \).

D. \( - \frac{\pi }{3} + k2\pi \).

Đáp án đúng là: A

Vì ABCDEF là lục giác đều nên

\(\widehat {AOB} = \widehat {BOC} = \widehat {COD} = \widehat {DOE} = \widehat {EOF} = \widehat {FOA} = \frac{{360^\circ }}{6} = 60^\circ = \frac{\pi }{3}\).

Khi đó, ta có: \(\left( {OA,OC} \right) = \frac{\pi }{3} + \frac{\pi }{3} + k2\pi = \frac{{2\pi }}{3} + k2\pi \).