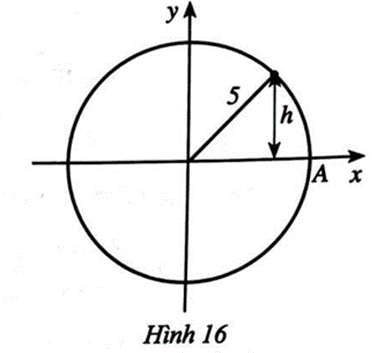
Một chất điểm chuyển động đều theo chiều ngược chiều kim đồng hồ trên đường tròn bán kính 5 cm. Khoảng cách h (cm) từ chất điểm đến trục hoành được tính theo công thức h = |y|, trong đó \(y = a\sin \left( {\frac{\pi }{5}t} \right)\) với t là thời gian chuyển động của chất điểm tính bằng giây (t ≥ 0) và chất điểm bắt đầu chuyển động từ vị trí A (Hình 16).

Tìm thời điểm sao cho chất điểm ở vị trí có h = 2,5 cm và nằm phía dưới trục hoành trong một vòng quay đầu tiên.

Từ kết quả câu b, ta có: \(y = 5\sin \left( {\frac{\pi }{5}t} \right)\).

Do h = 2,5 cm và chất điểm nằm ở dưới trục hoành nên y = – 2,5.

Với y = – 2,5, ta có: \(5\sin \left( {\frac{\pi }{5}t} \right) = - 2,5\)

\( \Leftrightarrow \sin \left( {\frac{\pi }{5}t} \right) = - \frac{1}{2}\)

\( \Leftrightarrow \sin \left( {\frac{\pi }{5}t} \right) = \sin \left( { - \frac{\pi }{6}} \right)\)

\( \Leftrightarrow \left[ \begin{array}{l}\frac{\pi }{5}t = - \frac{\pi }{6} + k2\pi \\\frac{\pi }{5}t = \pi - \left( { - \frac{\pi }{6}} \right) + k2\pi \end{array} \right.\,\,\left( {k \in \mathbb{Z}} \right)\)

\( \Leftrightarrow \left[ \begin{array}{l}t = \frac{{ - 5 + 60k}}{6}\\t = \frac{{35 + 60k}}{6}\end{array} \right.\,\,\,\left( {k \in \mathbb{Z}} \right)\)

Với vòng quay đầu tiên thì 0 ≤ t ≤ 10, do đó \(t = \frac{{35}}{6},\,\,t = \frac{{55}}{6}\).

Vậy tại thời điểm \(t = \frac{{35}}{6}\) giây, \(t = \frac{{55}}{6}\) giây thì chất điểm ở vị trí có h = 2,5 cm và nằm ở dưới trục hoành trong một vòng quay đầu tiên.