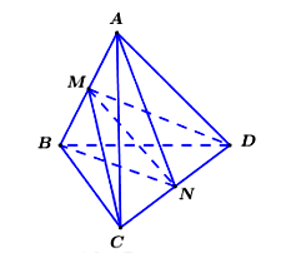
Cho khối tứ diện đều ABCD. Gọi M,N lần lượt là trung điểm của AB,CD.

Cho khối tứ diện đều ABCD. Gọi M,N lần lượt là trung điểm của AB,CD. Sử dụng mặt phẳng trung trực của AB và mặt phẳng trung trực của CD ta chia khối tứ diện đó thành bốn khối tứ diện nào sau đây?

B.$MANC,BCMN,AMND,MBND$

Trả lời

Phương pháp:

Sử dụng khái niệm mặt phẳng trung trực của đoạn thẳng là mặt phẳng vuông góc với đoạn thẳng tại trung điểm của đoạn thẳng đó.

Cách giải:

Vì ABCD là tứ diện đều nên các mặt của nó là tam giác đều.

Ta có: $\left\{\begin{array}{l}MD\perp AB\\ MC\perp AB\end{array}\right.\Rightarrow AB\perp \left(MCD\right)$ tại $M\Rightarrow \left(MCD\right)$ là mặt phẳng trung trực của AB.

Chứng minh tương tự ta có (NAB) là mặt phẳng trung trực của CD.

Khi đó $\left(MCD\right),\left(NAB\right)$ chia khối tứ diện thành bốn khối tứ diện: $MANC,BCMN,AMND,MBND$.

Chọn B.