Cho khối tứ diện đều ABCD cạnh a. Tính: Khoảng cách giữa hai đường thẳng AB và CD; Chiều cao và thể tích của khối tứ diện đều ABCD

Bài 54 trang 117 SBT Toán 11 Tập 2: Cho khối tứ diện đều ABCD cạnh a. Tính:

a) Khoảng cách giữa hai đường thẳng AB và CD;

b) Chiều cao và thể tích của khối tứ diện đều ABCD;

c) Côsin của góc giữa đường thẳng AB và mặt phẳng (BCD);

d) Côsin của số đo góc nhị diện [C, AB, D].

Trả lời

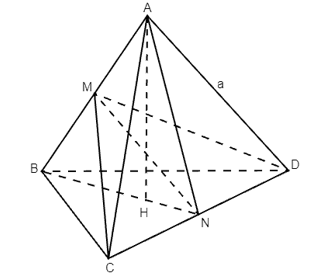
a) Do ABCD là tứ diện đều cạnh nên các tam giác ABC, ABD, ACD, BCD là các tam giác đều cạnh a.

Gọi M, N lần lượt là trung điểm của AB và CD nên $BM=AM=CN=DN=\frac{a}{2}.$

Xét tam giác ABC đều có CM là đường trung tuyến (do M là trung điểm AB).

Suy ra CM là đường cao của tam giác ABC hay CM ⊥ AB.

Chứng minh tương tự đối với các tam giác ABD, BCD, ACD đều ta có: DM ⊥ AB, BN ⊥ CD, AN ⊥ CD.

· Ta có: AB ⊥ CM, AB ⊥ DM, CM ∩ DM = M trong (CDM)

Suy ra AB ⊥ (CDM).

Mà MN ⊂ (CDM) nên AB ⊥ MN.

· Ta có: CD ⊥ BN, CD ⊥ AN, BN ∩ AN = N trong (ABN)

Suy ra CD ⊥ (ABN).

Mà MN ⊂ (ABN) nên CD ⊥ MN.

Ta có: AB ⊥ MN, CD ⊥ MN.

Suy ra MN là đoạn vuông góc chung của hai đường thẳng AB và CD.

Như vậy: d(AB, CD) = MN.

Áp dụng định lí Pythagore trong tam giác BCM vuông tại M có:

MC² = BC² – BM²

$\Rightarrow MC=\sqrt{B{C}^2–B{M}^2}=\sqrt{a^2-{\left(\frac{a}{2}\right)}^2}=\frac{a\sqrt{3}}{2}.$

Áp dụng định lí Pythagore trong tam giác CMN vuông tại N có:

CM² = MN² + CN²

$\Rightarrow MN=\sqrt{C{M}^2-C{N}^2}=\sqrt{{\left(\frac{a\sqrt{3}}{2}\right)}^2-{\left(\frac{a}{2}\right)}^2}=\frac{a\sqrt{2}}{2}.$

Vậy $d\left(AB,CD\right)=MN=\frac{a\sqrt{2}}{2}.$

b) Gọi H là hình chiếu của A trên (BCD) hay AH ⊥ (BCD).

Do ABCD là tứ diện đều, nên H là tâm đường tròn ngoại tiếp của tam giác BCD.

Vì tam giác BCD đều nên H cũng là trọng tâm của tam giác BCD.

Mà BN là đường trung tuyến của tam giác BCD (do N là trung điểm của CD)

Suy ra: H ∈ BN và $BH=\frac{2}{3}BN.$

Ta có: AH ⊥ (BCD), BH ⊂ (BCD) nên AH ⊥ BH.

Áp dụng định lí Pythagore trong tam giác BCN vuông tại N có:

BC² = BN­² + CN²

Suy ra $BN=\sqrt{B{C}^2-C{N}^2}=\sqrt{a^2-{\left(\frac{a}{2}\right)}^2}=\frac{a\sqrt{3}}{2}.$

Từ đó ta có $BH=\frac{2}{3}BN=\frac{2}{3}\cdot \frac{a\sqrt{3}}{2}=\frac{a\sqrt{3}}{3}.$

· Áp dụng định lí Pythagore trong tam giác ABH vuông tại H (do AH ⊥ BH) có:

AB² = AH² + BH²

Suy ra $AH=\sqrt{A{B}^2-B{H}^2}=\sqrt{a^2-{\left(\frac{a\sqrt{3}}{3}\right)}^2}=\frac{a\sqrt{6}}{3}.$

· Diện tích tam giác BCD là:

$S_{BCD}=\frac{1}{2}.BN.CD=\frac{1}{2}.\frac{a\sqrt{3}}{2}.a=\frac{a^2\sqrt{3}}{4}$(đvdt).

· Thể tích của khối tứ diện ABCD có đường cao $AH=\frac{a\sqrt{6}}{3},$ và diện tích đáy $S_{BCD}=\frac{a^2\sqrt{3}}{4}$ là:

$V_{ABCD}=\frac{1}{3}.\text{\hspace{0.17em}\hspace{0.17em}}{S}_{BCD}.AH=\frac{1}{3}.\frac{a^2\sqrt{3}}{4}.\frac{a\sqrt{6}}{3}=\frac{a^3\sqrt{2}}{12}$ (đvtt).

c) Do H là hình chiếu của A trên (BCD) nên góc giữa đường thẳng AB và mặt phẳng (BCD) bằng góc giữa hai đường thẳng AB và BH và bằng $\widehat{ABH}.$

Xét tam giác ABH vuông tại H có: $\cos \widehat{ABH}=\frac{BH}{AB}=\frac{\frac{a\sqrt{3}}{3}}{a}=\frac{\sqrt{3}}{3}.$

Vậy côsin của góc giữa đường thẳng AB và mặt phẳng (BCD) là $\frac{\sqrt{3}}{3}.$

d) Theo câu a ta có: CM ⊥ AB, DM ⊥ AB, CM ∩ DM = M ∈ AB.

Nên $\widehat{CMD}$ là góc phẳng nhị diện của góc nhị diện [C, AB, D].

Xét tam giác CMD, theo hệ quả định lí Côsin ta có:

$\cos \widehat{CMD}=\frac{C{M}^2+D{M}^2-C{D}^2}{2CM.DM}$

$\Rightarrow \cos \widehat{CMD}=\frac{{\left(\frac{a\sqrt{3}}{2}\right)}^2+{\left(\frac{a\sqrt{3}}{2}\right)}^2-a^2}{2.\frac{a\sqrt{3}}{2}.\frac{a\sqrt{3}}{2}}=\frac{1}{3}.$

Vậy côsin của số đo góc nhị diện [C, AB, D] bằng $\frac{1}{3}$

Xem thêm các bài giải SBT Toán lớp 11 Cánh diều hay, chi tiết khác:

Bài 2: Đường thẳng vuông góc với mặt phẳng

Bài 3: Góc giữa đường thẳng và mặt phẳng. Góc nhị diện

Bài 4: Hai mặt phẳng vuông góc

Bài 5: Khoảng cách

Bài 6: Hình lăng trụ đứng. Hình chóp đều. Thể tích của một số hình khối

Bài tập cuối chương 8