Cho khối chóp cụt đều ABC.A'B'C' có đường cao HH' = h, hai mặt đáy ABC, A'B'C'

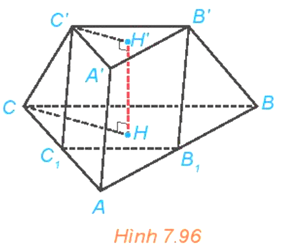
Luyện tập 2 trang 62 Toán 11 Tập 2: Cho khối chóp cụt đều ABC.A'B'C' có đường cao HH' = h, hai mặt đáy ABC, A'B'C' có cạnh tương ứng bằng 2a, a.

a)Tính thể tích khối chóp cụt.

b) Gọi B₁, C₁ tương ứng là trung điểm AB, AC. Chứng minh rằng AB₁C₁.A'B'C' là một hình lăng trụ. Tính thể tích khối lăng trụ AB₁C₁.A'B'C'.

Trả lời

a) Ta có $S_{A^{\text{'}}{B}^{\text{'}}{C}^{\text{'}}}=\frac{a^2\sqrt{3}}{4}$ ; $S_{ABC}=\frac{{\left(2a\right)}^2\sqrt{3}}{4}=a^2\sqrt{3}$ .

Khi đó $V_{ABC.A^{\text{'}}{B}^{\text{'}}{C}^{\text{'}}}=\frac{1}{3}\cdot \left(S_{ABC}+S_{A^{\text{'}}{B}^{\text{'}}{C}^{\text{'}}}+\sqrt{S_{ABC}\cdot S_{A^{\text{'}}{B}^{\text{'}}{C}^{\text{'}}}}\right)\cdot H{H}^{\text{'}}$

$=\frac{1}{3}\cdot \left(a^2\sqrt{3}+\frac{a^2\sqrt{3}}{4}+\sqrt{a^2\sqrt{3}\cdot \frac{a^2\sqrt{3}}{4}}\right)\cdot h$

$=\frac{1}{3}\cdot \left(a^2\sqrt{3}+\frac{a^2\sqrt{3}}{4}+\frac{a^2\sqrt{3}}{2}\right)\cdot h$.

b) Vì ABC.A'B'C' là khối chóp cụt đều nên (ABC) // (A'B'C') mà (AB₁C₁) $\subset$ (ABC) nên (AB₁C₁) // (A'B'C').

Xét tam giác ABC có B₁, C₁ lần lượt là trung điểm của AB, AC nên B₁C₁ là đường trung bình của tam giác ABC do đó B₁C₁ // BC và B₁C₁ = $\frac{BC}{2}=\frac{2a}{2}=a$.

Lại có B'C' // BC nên B₁C₁ // B'C' và B'C' = B₁C₁ = a nên B₁C₁C'B' là hình bình hành.

Vì B₁, C₁ lần lượt là trung điểm của AB, AC nên AB₁ = AC₁ = a.

Vì A'B' // AB₁ và A'B' = AB₁ = a nên A'B'B₁A là hình bình hành.

Vì A'C' // AC₁ và A'C' = AC₁ = a nên A'C'C₁A là hình bình hành.

Do đó AB₁C₁.A'B'C' là hình lăng trụ.

Vì hình lăng trụ AB₁C₁.A'B'C' có cùng chiều cao với khối chóp cụt đều ABC.A'B'C' nên $V_{A{B}_1{C}_1.A^{\text{'}}{B}^{\text{'}}{C}^{\text{'}}}=S_{A^{\text{'}}{B}^{\text{'}}{C}^{\text{'}}}.H{H}^{\text{'}}=\frac{a^2\sqrt{3}}{4}\cdot h$ .

Xem thêm các bài giải SGK Toán lớp 11 Kết nối tri thức hay, chi tiết khác: