Câu hỏi:
31/01/2024 68
Cho hình vẽ sau:
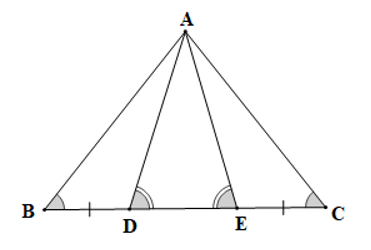
Cho các khẳng định sau:
(I) ∆ABD = ∆ACE;
(II) ∆ABE = ∆ACD;
Khẳng định đúng là:
Cho hình vẽ sau:
Cho các khẳng định sau:
(I) ∆ABD = ∆ACE;
(II) ∆ABE = ∆ACD;
Khẳng định đúng là:
A. Chỉ (I) đúng;
A. Chỉ (I) đúng;
B. Chỉ (II) đúng;
C. Cả (I) và (II) đều sai.
D. Cả (I) và (II) đều đúng.
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án đúng là: D.
• Ta có BD = CE (giả thiết)
Nên BD + DE = CE + DE
Suy ra BE = CD
Xét ∆ABE và ∆ACD có:
^AEB=^ADC(chứng minh trên),
BE = CD (chứng minh trên),
ˆB=ˆC (giả thiết)
Do đó ∆ABE = ∆ACD (g.c.g).
Vậy (I) đúng.
• Vì ∆ABE = ∆ACD (chứng minh trên)
Suy ra AB = AC
Xét ∆ABD và ∆ACE có:
AB = AC (chứng minh trên),
ˆB=ˆC (giả thiết),
BD = CE (giả thiết),
Do đó ∆ABD = ∆ACE (c.g.c)
Vậy (II) đúng.
Ta chọn phương án D.
Đáp án đúng là: D.
• Ta có BD = CE (giả thiết)
Nên BD + DE = CE + DE
Suy ra BE = CD
Xét ∆ABE và ∆ACD có:
^AEB=^ADC(chứng minh trên),
BE = CD (chứng minh trên),
ˆB=ˆC (giả thiết)
Do đó ∆ABE = ∆ACD (g.c.g).
Vậy (I) đúng.
• Vì ∆ABE = ∆ACD (chứng minh trên)
Suy ra AB = AC
Xét ∆ABD và ∆ACE có:
AB = AC (chứng minh trên),
ˆB=ˆC (giả thiết),
BD = CE (giả thiết),
Do đó ∆ABD = ∆ACE (c.g.c)
Vậy (II) đúng.
Ta chọn phương án D.
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Cho tam giác ABC nhọn. Qua A kẻ đường thẳng song song với BC, qua B kẻ đường thẳng song song với AC, hai đường thẳng này cắt nhau tại D. Giao điểm của AB với CD là O. Khẳng định nào sau đây là sai:
Cho tam giác ABC nhọn. Qua A kẻ đường thẳng song song với BC, qua B kẻ đường thẳng song song với AC, hai đường thẳng này cắt nhau tại D. Giao điểm của AB với CD là O. Khẳng định nào sau đây là sai:
Câu 2:
Cho hình vẽ dưới đây:
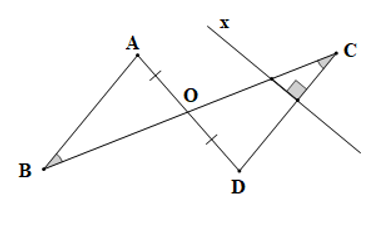
Xét các khẳng định:
(1) BA = CD;
(2) x ⊥ BA.
Chọn câu đúng:
Cho hình vẽ dưới đây:
Xét các khẳng định:
(1) BA = CD;
(2) x ⊥ BA.
Chọn câu đúng:
Câu 3:
Điền vào chỗ còn thiếu trong các bước chứng minh sau:
“Xét ∆ABC và ∆MNP có:
.............,
BC = PN.
^ABC=^MNP;
Vậy ∆ABC = ∆MNP (g.c.g)”
Điền vào chỗ còn thiếu trong các bước chứng minh sau:
“Xét ∆ABC và ∆MNP có:
.............,
BC = PN.
^ABC=^MNP;
Vậy ∆ABC = ∆MNP (g.c.g)”
Câu 4:
Cho tam giác HIK, A là trung điểm của IH. Đường thẳng qua A và song song với HK cắt IK tại B. Đường thẳng qua B và song song với IH cắt HK tại C. Khẳng định nào sau đây là đúng nhất ?
Cho tam giác HIK, A là trung điểm của IH. Đường thẳng qua A và song song với HK cắt IK tại B. Đường thẳng qua B và song song với IH cắt HK tại C. Khẳng định nào sau đây là đúng nhất ?
Câu 6:
Cho góc xOy nhọn. Trên tia phân giác của góc xOy lấy điểm I tuỳ ý, qua I vẽ đường thẳng vuông góc với OI, cắt Ox ở A và cắt Oy ở B. Khẳng định nào sau đây là đúng?
Cho góc xOy nhọn. Trên tia phân giác của góc xOy lấy điểm I tuỳ ý, qua I vẽ đường thẳng vuông góc với OI, cắt Ox ở A và cắt Oy ở B. Khẳng định nào sau đây là đúng?
Câu 7:
Cho góc xOy, Oz là tia phân giác của góc đó. Gọi I là một điểm trên tia Oz (I khác O). Kẻ IM vuông góc với Ox (M ∈ Ox), IN vuông góc với Oy (N ∈ Oy). Biết độ dài đoạn thẳng IM là 2 cm, độ dài đoạn thẳng IN là:
Cho góc xOy, Oz là tia phân giác của góc đó. Gọi I là một điểm trên tia Oz (I khác O). Kẻ IM vuông góc với Ox (M ∈ Ox), IN vuông góc với Oy (N ∈ Oy). Biết độ dài đoạn thẳng IM là 2 cm, độ dài đoạn thẳng IN là:
Câu 9:
Cho tứ giác MNPQ, MN // PQ, MN = PQ, I là giao điểm của MP và NQ. Cho các khẳng định sau:
(1) MQ = NP;
(2) IM = IP;
(3) IN = IQ.
Số khẳng định sai là:
Cho tứ giác MNPQ, MN // PQ, MN = PQ, I là giao điểm của MP và NQ. Cho các khẳng định sau:
(1) MQ = NP;
(2) IM = IP;
(3) IN = IQ.
Số khẳng định sai là:
Câu 10:
Cho tam giác FDE và tam giác MNP có ˆF=ˆP,ˆE=ˆN, FE = NP. Biết ˆF+ˆE=155° số đo góc M là:
Cho tam giác FDE và tam giác MNP có ˆF=ˆP,ˆE=ˆN, FE = NP. Biết ˆF+ˆE=155° số đo góc M là:
Câu 12:
Cho ABC và MNP có Để ABC = MNP theo trường hợp góc – cạnh – góc thì phải thêm điều kiện nào sau đây:
Cho ABC và MNP có Để ABC = MNP theo trường hợp góc – cạnh – góc thì phải thêm điều kiện nào sau đây:
Câu 14:
Cho hình thang cân MNPQ như hình vẽ sau:
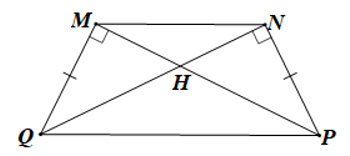
Trong hình bên có mấy cặp tam giác vuông bằng nhau?
Cho hình thang cân MNPQ như hình vẽ sau:
Trong hình bên có mấy cặp tam giác vuông bằng nhau?


