Cho hình tứ diện vuông OABC có các cạnh OA, OB, OC bằng nhau và lần lượt nằm trên các trục Ox, Oy, Oz
91
22/02/2024
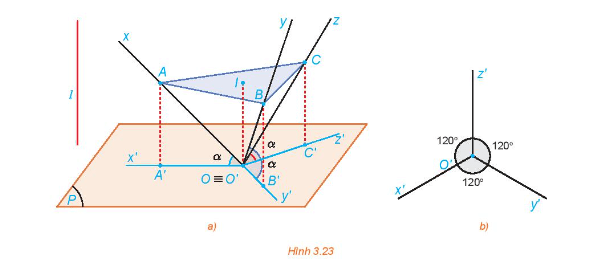
HĐ7 trang 62 Chuyên đề Toán 11: Cho hình tứ diện vuông OABC có các cạnh OA, OB, OC bằng nhau và lần lượt nằm trên các trục Ox, Oy, Oz đôi một vuông góc. Xét phép chiếu vuông góc lên mặt phẳng (P) đi qua O sao cho các trục Ox, Oy, Oz tạo với (P) các góc bằng nhau (H.3.23a). Gọi A', B', C' lần lượt là hình chiếu của A, B, C.
a) Chứng minh rằng ABC là tam giác đều.
b) Giải thích tại sao các khoảng cách từ A, B, C đến (P) bằng nhau, từ đó suy ra mặt phẳng (ABC) song song với mặt phẳng (P).
c) Gọi I là tâm tam giác đều ABC. Giải thích tại sao A' , từ đó suy ra .
Trả lời
a) Ta có: OA = OB = OC, .
Suy ra các tam giác AOB, BOC và COA bằng nhau từng đôi một.
Từ đó suy ra AB = BC = CA nên tam giác ABC là tam giác đều.
b) Ta có: OA = OB = OC; ; .
Do đó, các tam giác AA'O, BB'O và CCO' bằng nhau từng đôi một.
Từ đó suy ra AA' = BB' = CC'.
Do đó, khoảng cách từ A, B, C đến (P) bằng nhau.
Ta có: AA' = BB', AA' // BB' nên ABB'A' là hình bình hành.
Suy ra: AB // A'B'.
Tương tự ta chứng minh BC // B'C'; CA // C'A'
Mà A'B', B'C', C'A' thuộc (P)
Suy ra: (ABC) song song với (P).
c) Dễ dàng chứng minh được IA = O'A' (AIO'A' là hình bình hành).
Tương tự IB = O'B', AB = A'B'.
Do đó ∆IAB = ∆O'A'B' (c.c.c).
Suy ra .
Tương tự, ta chứng minh được
Do I là tâm tam giác đều ABC nên dễ dàng chứng minh được .
Nên suy ra .
Vậy .
Xem thêm các bài giải Chuyên đề Toán lớp 11 Kết nối tri thức hay, chi tiết khác:

