Cho hình tứ diện ABCD có AB = a, BC = b, BD = c. Gọi M, N, P lần lượt là trung điểm của AB, AC, AD

Bài 2 trang 106 Toán 11 Tập 2:Cho hình tứ diện ABCD có AB = a, BC = b, BD = c, $\widehat{ABC}=\widehat{ABD}=\widehat{BCD}=90°.$ Gọi M, N, P lần lượt là trung điểm của AB, AC, AD (Hình 77).

a) Tính khoảng cách từ điểm C đến đường thẳng AB.

b) Tính khoảng cách từ điểm D đến mặt phẳng (ABC).

c) Tính khoảng cách giữa hai đường thẳng AB và CD.

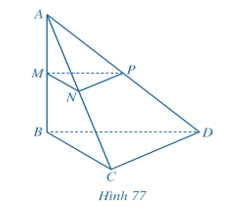
Trả lời

a) Vì $\widehat{ABC}=90°$ nên CB ⊥ AB.

Suy ra d(C, AB) = CB = b.

Vậy khoảng cách từ điểm C đến đường thẳng AB bằng b.

b) Vì $\widehat{ABD}=90°$ nên AB ⊥ BD.

Ta có: AB ⊥ CB, AB ⊥ BD và CB ∩ BD = B trong (BCD).

Suy ra AB ⊥ (BCD).

Mà CD ⊂ (BCD) nên AB ⊥ CD.

Vì $\widehat{BCD}=90°$ nên CD ⊥ BC.

Ta có: CD ⊥ AB, CD ⊥ BC và AB ∩ BC = B trong (ABC).

Suy ra CD ⊥ (ABC).

Khi đó d(D, (ABC)) = CD.

Áp dụng định lí Pythagore vào tam giác BCD vuông tại C có:

BD² = BC² + CD²

Suy ra $CD=\sqrt{B{D}^2-B{C}^2}=\sqrt{c^2-b^2}.$

Do đó $d\left(D,\left(ABC\right)\right)=CD=\sqrt{c^2-b^2}.$

Vậy khoảng cách từ điểm D đến mặt phẳng (ABC) bằng $\sqrt{c^2-b^2}.$

c) Ta có: BC ⊥ AB (theo câu a) và BC ⊥ CD (theo câu b).

Suy ra đoạn thẳng BC là đoạn vuông góc chung của hai đường thẳng AB và CD.

Do đó d(AB, CD) = BC = b.

Vậy khoảng cách giữa hai đường thẳng AB và CD bằng b.

Xem thêm các bài giải SGK Toán lớp 11 Cánh diều hay, chi tiết khác: