Cho hình thang cân ABCD có đáy lớn AD và đáy nhỏ BC thỏa mãn AD = 4 cm và AB = BC = CD = 2 cm (H.4.62). Tính các góc

Bài 4.60 trang 74 Tập 1: Cho hình thang cân ABCD có đáy lớn AD và đáy nhỏ BC thỏa mãn AD = 4 cm và AB = BC = CD = 2 cm (H.4.62). Tính các góc của hình thang ABCD.

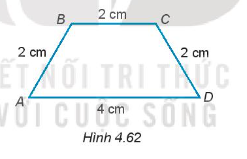
Trả lời

Gọi O là trung điểm của AD.

Khi đó, AO = OD = $\frac{AD}{2}=\frac{4}{2}=2$ (cm).

Do đó, AB = BC = CD = AO = OD = 2 cm.

Tam giác ABO có AB = BO nên tam giác ABO cân tại đỉnh A.

Suy ra $\widehat{ABO}=\widehat{AOB}$.

Lại có: AD // BC (do ABCD là hình thang cân có AD và BC là đáy)

Suy ra $\widehat{CBO}=\widehat{AOB}$ (hai góc so le trong).

Do đó, $\widehat{ABO}=\widehat{AOB}=\widehat{CBO}$.

Xét tam giác ABO và tam giác CBO có:

AB = BC (= 2 cm)

$\widehat{ABO}=\widehat{CBO}$ (cmt)

BO: cạnh chung

Do đó, ∆ABO = ∆CBO (c – g – c).

Suy ra CO = AO = 2 cm.

Tam giác COD có CD = OD = OC (= 2 cm). Do đó tam giác COD là tam giác đều.

Suy ra $\widehat{D}=\widehat{CDO}=60°$.

Ta có: $\widehat{D}+\widehat{BCD}=180°$ (BC // AD, hai góc ở vị trí trong cùng phía)

Suy ra $\widehat{BCD\text{}}=180°-\widehat{D}$$=180°-60°=120°$.

Do ABCD là hình thang cân với AD và BC là đáy.

Vậy $\widehat{A}=\widehat{D}=60°$ và $\widehat{ABC}=\widehat{BCD}=120°$.

Xem thêm các bài giải SBT Toán lớp 7 Kết nối tri thức hay, chi tiết khác:

Bài 15: Các trường hợp bằng nhau của tam giác vuông

Bài 16: Tam giác cân. Đường trung trực của đoạn thẳng

Ôn tập chương 4

Bài 17: Thu thập và phân loại dữ liệu

Bài 18: Biểu đồ hình quạt tròn

Bài 19: Biểu đồ đoạn thẳng