Câu hỏi:
03/04/2024 54
Cho hình lập phương ABCD.A'B'C'D'. Gọi M, N, P lần lượt là trung điểm các cạnh AB, BC, C'D'. Tính góc giữa hai đường thẳng MN và AP.
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
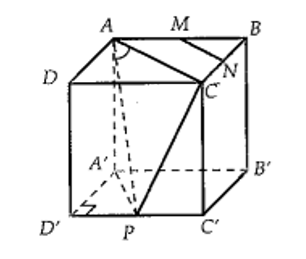
Giả sử hình lập phương có cạnh bằng a và MN // AC nên: (^MN,AP)=(^AC,AP)
Vì ΔA' vuông tại D' nên
vuông tại A' nên
vuông tại C' nên
Ta có AC là đường chéo của hình vuông ABCD nên
Áp dụng định lý cosin trong tam giác ACP ta có:
Vậy hay

Giả sử hình lập phương có cạnh bằng a và MN // AC nên: (^MN,AP)=(^AC,AP)
Vì ΔA' vuông tại D' nên
vuông tại A' nên
vuông tại C' nên
Ta có AC là đường chéo của hình vuông ABCD nên
Áp dụng định lý cosin trong tam giác ACP ta có:
Vậy hay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 2:
Cho hình chóp S.ABCD, có bao nhiêu vectơ khác vectơ mà có điểm đầu và điểm cuối là các đỉnh của hình chóp.
Xem đáp án »
03/04/2024
69
Câu 3:
Cho tứ diện ABCD có AB = AC, DB = DC. Khẳng định nào sau đây đúng?
Xem đáp án »
03/04/2024
67
Câu 4:
Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng a. Khi đó góc giữa A'C' và BD bằng
Xem đáp án »
03/04/2024
67
Câu 9:
Cho hàm số . Chỉ ra các điểm gián đoạn của hàm số trên khoảng (0; 2021)?
Xem đáp án »
03/04/2024
65


