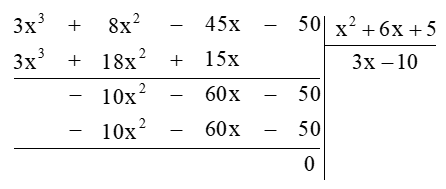Cho hình hộp chữ nhật có thể tích bằng V = 3x^3 + 8x^2 – 45x – 50 (cm^3)

Bài 10 trang 33 SBT Toán 7 Tập 2:

Cho hình hộp chữ nhật có thể tích bằng V = 3x³ + 8x² – 45x – 50 (cm³), chiều dài bằng (x + 5) cm và chiều cao (x + 1) cm. Hãy tính chiều rộng của hình hộp chữ nhật.

Trả lời

Gọi a (cm, a > 0) là chiều rộng của hình hộp chữ nhật.

Khi đó thể tích của hình hộp chữ nhật là:

V = (x + 5) . (x + 1) . a

    = (x² + x + 5x + 5) . a

    = (x² + 6x + 5) . a (cm³)

Mà theo bài hình hộp chữ nhật có thể tích V = 3x³ + 8x² – 45x – 50 (cm³) nên ta có:

(x² + 6x + 5) . a = 3x³ + 8x² – 45x – 50

Suy ra: $a=\frac{3x^3+8x^2-45x-50}{x^2+6x+5}.$

Ta thực hiện đặt tính phép chia đa thức:

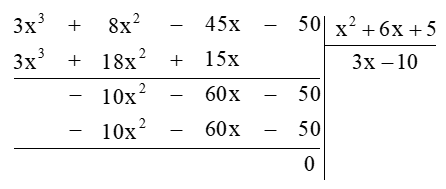
Khi đó  $a=\frac{3x^3+8x^2-45x-50}{x^2+6x+5}=3x-10.$

Vậy chiều rộng của hình hộp chữ nhật là 3x – 10 (cm).

Xem thêm lời giải sách bài tập Toán lớp 7 Chân trời sáng tạo hay, chi tiết khác:

Bài 2: Đa thức một biến

Bài 3: Phép cộng và phép trừ đa thức một biến

Bài 4: Phép nhân và phép chia đa thức một biến

Bài tập cuối chương 7

Bài 1: Góc và cạnh của một tam giác

Bài 2: Tam giác bằng nhau