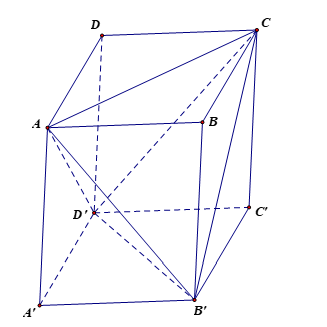
Cho hình hộp ABCD.A'B'C'D' có các cạnh bằng nhau. Chứng minh rằng tứ diện ACB'D' có các cặp cạnh đối diện vuông góc với nhau.

Vì hình hộp ABCD.A'B'C'D' có các cạnh bằng nhau nên các mặt của hình hộp là hình thoi.

Vì ABB'A' là hình thoi nên AB' ^ A'B.

Có CB // A'D' và CB = A'D' (do cùng song song và bằng AD). Do đó CBA'D' là hình bình hành, suy ra CD' // BA'.

Khi đó (CD', AB') = (BA', AB') = 90°.

Vậy CD' và AB' vuông góc với nhau.

Vì ADD'A' là hình thoi nên AD' ^ A'D.

Có CD // A'B' và CD = A'B' (vì CD, A'B' cùng song song và bằng AB) nên CDA'B' là hình bình hành, suy ra CB' // DA'.

Khi đó (CB', AD') = (DA', AD') = 90°.

Vậy CB' và AD' vuông góc với nhau.

Do ABCD là hình thoi nên AC ^ BD.

Vì BB' // DD' và BB' = DD' (do BB', DD' cùng song song và bằng AA' ) nên BDD'B' là hình bình hành, suy ra BD // B'D'.

Khi đó (AC, B'D') = (AC, BD) = 90°.

Vậy AC và B'D' vuông góc với nhau.