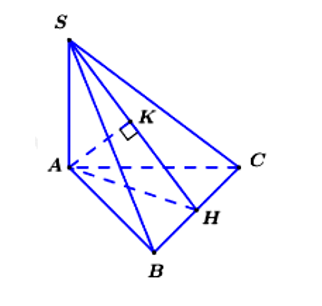
Cho hình chóp tam giác S.ABCD có đáy tam giác vuông tại A, SA vuông góc (ABC)

Cho hình chóp tam giác S.ABCD có đáy tam giác vuông tại $A,SA\perp \left(ABC\right).$ Biết mặt bên (SBC) tạo với đáy một góc ${45}^0$ và $AB=AC=2a.$ Tính theo a khoảng cách từ A đến mặt phẳng (SBC).

Trả lời

Phương pháp:

- Gọi H là trung điểm của BC chứng minh $BC\perp \left(SAH\right).$

- Trong (SAH) kẻ $AK\perp SH,$ chứng minh $AK\perp \left(SBC\right)\Rightarrow d\left(A:\left(SBC\right)\right)=AK.$

- Xác định góc giữa (SBC) và (ABC) là góc giữa hai đường thẳng lần lượt thuộc hai mặt phẳng và cùng vuông góc với giao tuyến.

- Tính AH Sử dụng tính chất tam giác vuông cân hoặc hệ thức lượng trong tam giác vuông tính AK

Cách giải:

Gọi H là trung điểm của BC vì $\Delta ABC$ vuông cân tại A nên $AH\perp BC$ và $AH=\frac{AB}{\sqrt{2}}=a\sqrt{2}.$

Ta có: $\left\{\begin{array}{l}BC\perp AH\\ BC\perp SA\end{array}\right.\Rightarrow BC\perp \left(SAH\right).$

Trong (SAH) kẻ $AK\perp SH,$ ta có: $\left\{\begin{array}{l}AK\perp SH\\ AK\perp SB\left(SB\perp \left(SAH\right)\right)\end{array}\right.\Rightarrow AK\perp \left(SBC\right)\Rightarrow d\left(A;\left(SBC\right)\right)=AK.$

Ta có: $BC\perp \left(SAH\right)\Rightarrow BC\perp SH,$ khi đó ta có: $\left\{\begin{array}{l}\left(SBC\right)\cap \left(ABC\right)=BC\\ SH\subset \left(SBC\right),SH\perp BC\left(cmt\right)\\ AH\subset \left(ABC\right),AH\perp BC\left(cmt\right)\end{array}\right.$

$\Rightarrow \angle \left(\left(SBC\right);\left(ABC\right)\right)=\angle \left(SH;AH\right)=\angle SHA={45}^0.$

$\Rightarrow \Delta AKH$ vuông cân tại $K\Rightarrow AK=\frac{AH}{\sqrt{2}}=a.$

Vậy $d\left(A;\left(SBC\right)\right)=a.$

Chọn B.