Câu hỏi:
03/04/2024 37
Cho hình chóp S.ABCD, đáy ABCD là hình bình hành, cắt hình chóp bằng mặt phẳng (MNP), trong đó M, N, P lần lượt là trung điểm các cạnh AB, AD, SC. Thiết diện nhận được là
Cho hình chóp S.ABCD, đáy ABCD là hình bình hành, cắt hình chóp bằng mặt phẳng (MNP), trong đó M, N, P lần lượt là trung điểm các cạnh AB, AD, SC. Thiết diện nhận được là
A. ngũ giác
B. tứ giác
C. tam giác
D. không có
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án A
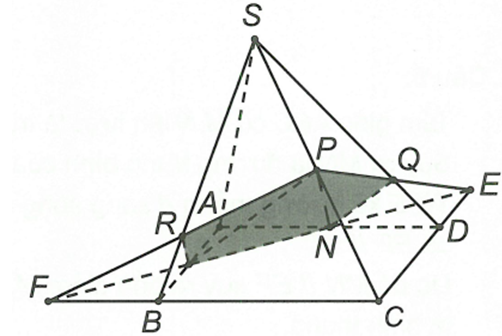
Trong mp (ABCD) gọi
Gọi . Suy ra thiết diện tao bởi mặt phẳng (MNP) với hình chóp là ngũ giác MNQPR.
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Cho tứ diện đều ABCD có cạnh bằng a. Gọi G là trọng tâm tam giác ABC. Mặt phẳng (GCD) cắt tứ diện theo một thiết diện có diện tích
Cho tứ diện đều ABCD có cạnh bằng a. Gọi G là trọng tâm tam giác ABC. Mặt phẳng (GCD) cắt tứ diện theo một thiết diện có diện tích
Câu 2:
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi I, J lần lượt là trung điểm của SB và SD. Thiết diện của mặt phẳng (AIJ) với hình chóp là
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi I, J lần lượt là trung điểm của SB và SD. Thiết diện của mặt phẳng (AIJ) với hình chóp là
Câu 3:
Cho tứ diện ABCD. Gọi I, J lần lượt là các điểm nằm trên AB, AD sao cho BD và IJ không song song. Tìm thiết diện tạo bởi (CU) và hình chóp
Cho tứ diện ABCD. Gọi I, J lần lượt là các điểm nằm trên AB, AD sao cho BD và IJ không song song. Tìm thiết diện tạo bởi (CU) và hình chóp
Câu 4:
Cho hình chóp S.ABCD (AB và CD không song song) và M là điểm nằm trong ∆SCD. Xác định thiết diện của hình chóp cắt bởi mặt phẳng (ABM)
Cho hình chóp S.ABCD (AB và CD không song song) và M là điểm nằm trong ∆SCD. Xác định thiết diện của hình chóp cắt bởi mặt phẳng (ABM)
Câu 5:
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Trong mặt phẳng (ABCD) vẽ đường thẳng d đi qua A và không song song với các cạnh của hình bình hành. Trên cạnh SC lấy điểm M. Tìm thiết diện của hình chóp khi cắt bởi mặt phẳng (M,d).
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Trong mặt phẳng (ABCD) vẽ đường thẳng d đi qua A và không song song với các cạnh của hình bình hành. Trên cạnh SC lấy điểm M. Tìm thiết diện của hình chóp khi cắt bởi mặt phẳng (M,d).
Câu 6:
Cho hình chóp S.ABCD. M là điểm thuộc cạnh SB (không trùng với S và B). Thiết diện tạo bởi (AMD) và hình chóp S.ABCD là
Cho hình chóp S.ABCD. M là điểm thuộc cạnh SB (không trùng với S và B). Thiết diện tạo bởi (AMD) và hình chóp S.ABCD là
Câu 7:
Cho tứ diện ABCD và ba điểm M, N, P lần lượt nằm trên các cạnh AB, AC, AD (không trùng với các đỉnh). Thiết diện của tứ diện cắt bởi mặt phẳng (MNP) là
Cho tứ diện ABCD và ba điểm M, N, P lần lượt nằm trên các cạnh AB, AC, AD (không trùng với các đỉnh). Thiết diện của tứ diện cắt bởi mặt phẳng (MNP) là
Câu 8:
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M, N, P là các điểm lần lượt trên các cạnh CB, CD, SA. Tìm thiết diện của hình chóp cắt bởi mặt phẳng (MNP)
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M, N, P là các điểm lần lượt trên các cạnh CB, CD, SA. Tìm thiết diện của hình chóp cắt bởi mặt phẳng (MNP)
Câu 9:
Cho hình chóp S.ABCD có đáy ABCD là hình thang, đáy lớn AB. Gọi M, N lần lượt là trung điểm của SB và SC.
a) Tìm giao tuyến của hai mặt phẳng (SAD) và (SBC)
Cho hình chóp S.ABCD có đáy ABCD là hình thang, đáy lớn AB. Gọi M, N lần lượt là trung điểm của SB và SC.
a) Tìm giao tuyến của hai mặt phẳng (SAD) và (SBC)
Câu 11:
Cho tứ diện ABCD có M, N lần lượt là trung điểm của AB, CD và P là một điểm thuộc cạnh BC (P không trùng trung điểm cạnh BC). Tìm thiết diện của tứ diện cắt bởi mặt phẳng (MNP).
Cho tứ diện ABCD có M, N lần lượt là trung điểm của AB, CD và P là một điểm thuộc cạnh BC (P không trùng trung điểm cạnh BC). Tìm thiết diện của tứ diện cắt bởi mặt phẳng (MNP).
Câu 12:
Cho tứ diện ABCD; gọi M, N lần lượt là trung điểm các cạnh AB và AC, E là điểm trên cạnh CD với ED = 3EC. Thiết diện tạo bởi mặt phẳng (MNE) và tứ diện ABCD
Cho tứ diện ABCD; gọi M, N lần lượt là trung điểm các cạnh AB và AC, E là điểm trên cạnh CD với ED = 3EC. Thiết diện tạo bởi mặt phẳng (MNE) và tứ diện ABCD


