Câu hỏi:
13/03/2024 54
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, SA vuông góc với đáy và SA = 2a, M là trung điểm của SD. Tính khoảng cách giữa đường thẳng SB và mặt phẳng (ACM).
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, SA vuông góc với đáy và SA = 2a, M là trung điểm của SD. Tính khoảng cách giữa đường thẳng SB và mặt phẳng (ACM).
A.
B. a
C.
D.
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án đúng là: C
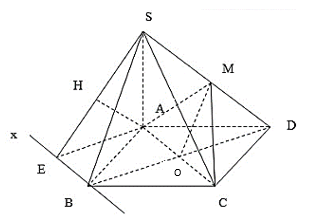
Gọi O là giao điểm của AC, BD. Khi đó O là trung điểm của AC, BD.
Vì O, M lần lượt là trung điểm của BD, SD nên OM là đường trung bình của DSBD.
Suy ra OM // SB Þ SB // (AMC) (1).
Qua B, kẻ Bx // AC và qua A kẻ AE vuông góc với Bx tại E. Suy ra BE // (AMC) (2).
Từ (1) và (2), suy ra (SBE) // (AMC).
Kẻ AH ^ SE (3).
Vì AE ^ EB mà SA ^ EB (do SA ^ (ABCD)) Þ EB ^ (SAE) Þ EB ^ AH (4).
Từ (3), (4) Þ AH ^ (SEB).
Ta có d(SB, (ACM)) = d((SBE), (ACM)) = d(A, (SBE)) = AH.
Xét DABD vuông tại A, có .
Ta có .
Xét DSAE vuông tại A, có .
Đáp án đúng là: C

Gọi O là giao điểm của AC, BD. Khi đó O là trung điểm của AC, BD.
Vì O, M lần lượt là trung điểm của BD, SD nên OM là đường trung bình của DSBD.
Suy ra OM // SB Þ SB // (AMC) (1).
Qua B, kẻ Bx // AC và qua A kẻ AE vuông góc với Bx tại E. Suy ra BE // (AMC) (2).
Từ (1) và (2), suy ra (SBE) // (AMC).
Kẻ AH ^ SE (3).
Vì AE ^ EB mà SA ^ EB (do SA ^ (ABCD)) Þ EB ^ (SAE) Þ EB ^ AH (4).
Từ (3), (4) Þ AH ^ (SEB).
Ta có d(SB, (ACM)) = d((SBE), (ACM)) = d(A, (SBE)) = AH.
Xét DABD vuông tại A, có .
Ta có .
Xét DSAE vuông tại A, có .
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Cho hình lăng trụ tam giác ABC.A'B'C' có các cạnh bên hợp với đáy những góc bằng 60°, đáy ABC là tam giác đều và A' cách đều A, B, C. Tính khoảng cách giữa hai đáy của hình lăng trụ.
Cho hình lăng trụ tam giác ABC.A'B'C' có các cạnh bên hợp với đáy những góc bằng 60°, đáy ABC là tam giác đều và A' cách đều A, B, C. Tính khoảng cách giữa hai đáy của hình lăng trụ.
Câu 2:
Cho hình lăng trụ tứ giác đều ABCD. A'B'C'D' có cạnh đáy bằng a. Gọi M, N, P lần lượt là trung điểm của AD, DC, A'D'. Tính khoảng cách giữa hai mặt phẳng (MNP) và (ACC').
Cho hình lăng trụ tứ giác đều ABCD. A'B'C'D' có cạnh đáy bằng a. Gọi M, N, P lần lượt là trung điểm của AD, DC, A'D'. Tính khoảng cách giữa hai mặt phẳng (MNP) và (ACC').
Câu 3:
Cho hình thang vuông ABCD vuông ở A và D, AD = 2a. Trên đường thẳng vuông góc tại D với (ABCD) lấy điểm S với . Tính khoảng cách giữa đường thẳng DC và (SAB).
Cho hình thang vuông ABCD vuông ở A và D, AD = 2a. Trên đường thẳng vuông góc tại D với (ABCD) lấy điểm S với . Tính khoảng cách giữa đường thẳng DC và (SAB).
Câu 4:
Cho hình chóp tứ giác đều S.ABCD có AB = SA = 2a. Khoảng cách từ đường thẳng AB đến (SCD) bằng bao nhiêu?
Cho hình chóp tứ giác đều S.ABCD có AB = SA = 2a. Khoảng cách từ đường thẳng AB đến (SCD) bằng bao nhiêu?
Câu 5:
Cho hình chóp O.ABC có đường cao . Gọi M và N lần lượt là trung điểm của OA và OB. Khoảng cách giữa đường thẳng MN và (ABC) bằng:
Câu 6:
Cho hình lập phương ABCD.A'B'C'D' cạnh a. Khoảng cách giữa (ACB') và (DA'C') bằng
Cho hình lập phương ABCD.A'B'C'D' cạnh a. Khoảng cách giữa (ACB') và (DA'C') bằng
Câu 7:
Cho hình lăng trụ tam giác ABC.A'B'C' có cạnh bên bằng a. Các cạnh bên của lăng trụ tạo với mặt đáy góc 60°. Hình chiếu vuông góc của A' lên mặt phẳng (ABC) là trung điểm của BC. Khoảng cách giữa hai mặt đáy của lăng trụ bằng bao nhiêu?
Cho hình lăng trụ tam giác ABC.A'B'C' có cạnh bên bằng a. Các cạnh bên của lăng trụ tạo với mặt đáy góc 60°. Hình chiếu vuông góc của A' lên mặt phẳng (ABC) là trung điểm của BC. Khoảng cách giữa hai mặt đáy của lăng trụ bằng bao nhiêu?
Câu 8:
Cho hình chóp tứ giác đều S.ABCD có tất cả các cạnh bằng a. Khi đó khoảng cách giữa đường thẳng AB và mặt phẳng (SCD) bằng
Cho hình chóp tứ giác đều S.ABCD có tất cả các cạnh bằng a. Khi đó khoảng cách giữa đường thẳng AB và mặt phẳng (SCD) bằng
Câu 9:
Cho hình hộp chữ nhật ABCD.A'B'C'D' có AB = 4, AD = 3. Mặt phẳng (ACD') tạo với mặt đáy một góc 60°. Tính khoảng cách giữa hai mặt đáy của hình hộp.
Cho hình hộp chữ nhật ABCD.A'B'C'D' có AB = 4, AD = 3. Mặt phẳng (ACD') tạo với mặt đáy một góc 60°. Tính khoảng cách giữa hai mặt đáy của hình hộp.


