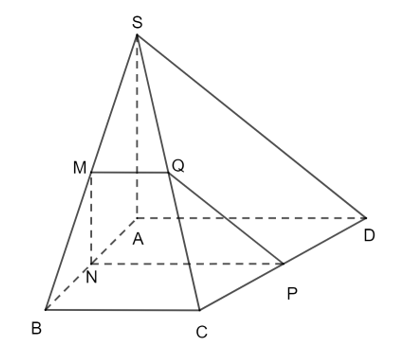
Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông với AB là cạnh góc vuông và có cạnh SA vuông góc với mặt phẳng (ABCD). Cho M, N, P, Q lần lượt là trung điểm của SB, AB, CD, SC. Chứng minh rằng:
a) AB ⊥ (MNPQ);

a) Xét tam giác SBC:

M là trung điểm SB

Q là trung điểm SC

Do đó MQ là đường trung bình của ΔSBC.

$\left.\begin{array}{c}MQ//BC\\ BC\perp AB\end{array}\right\}\Rightarrow MQ\perp \text{AB}$ (1)

Tương tự: MN là đường trung bình của ΔSAB. Khi đó:

 $\left.\begin{array}{c} MN // SA\\ SA\perp \left(ABCD\right)\end{array}\right\}\Rightarrow$ MN ⊥ (ABCD)  MN ⊥ AB (2)

Xét hình thang ABCD:

N là trung điểm AB

P là trung điểm CD

Do đó NP là đường trung bình của hình thang ABCD. Khi đó:

$\left.\begin{array}{c}NP // BC\\ BC \perp AB\end{array}\right\} \Rightarrow NP \perp \text{AB}$

Từ (1), (2) và (3) suy ra AB ⊥ (MNPQ)