Bài 4 trang 94 Toán 11 Tập 1: Cho hình chóp S.ABCD có AC cắt BD tại O và AB cắt CD tại P. Điểm M thuộc cạnh SA (M khác S, M khác A). Gọi N là giao điểm của MP và SB, I là giao điểm của MC và DN. Chứng minh rằng S, O, I thẳng hàng.
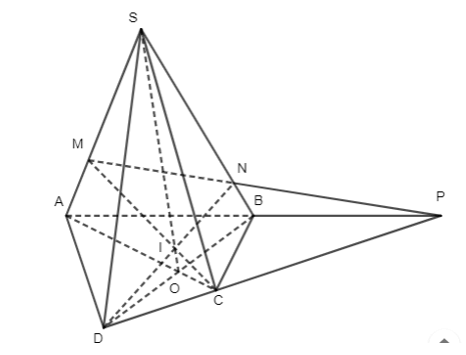
• Ta có: S ∈ (SAC) và S ∈ (SBD)
Do đó S là giao điểm của (SAC) và (SBD).
Mặt khác: AC ∩ BD = {O}.
AC ⊂ (SAC);
BD ⊂ (SBD).
Do đó O là giao điểm của (SAC) và (SBD).
Suy ra (SAC) ∩ (SBD) = SO.
• Trong mặt phẳng (DMNC) có:
DN ∩ MC = {I}.
DN ⊂ (SDB);
MC ⊂ (SAB).
Do đó I là giao điểm của (SAC) và (SBD).
Suy ra giao tuyến SO của hai mặt phẳng này đi qua điểm I.
Hay I ∈ SO.
Vậy S, I, O thẳng hàng.
Xem thêm các bài giải SGK Toán lớp 11 Cánh diều hay, chi tiết khác:
Bài 1: Đường thẳng và mặt phẳng trong không gian
Bài 2: Hai đường thẳng song song trong không gian