Bài 4.8 trang 56 SBT Toán 11 Tập 1: Cho hình tứ diện SABC và các điểm A’,B’,C’ lần lượt thuộc các cạnh SA, SB, SC. Giả sử hai đường thẳng B’C’ và BC cắt nhau tại D, hai đường thẳng C’A’ và CA cắt nhau tại E và hai đường thẳng A’B’ và AB cắt nhau tại F. Chứng minh rằng ba điểm D, E, F thẳng hàng.
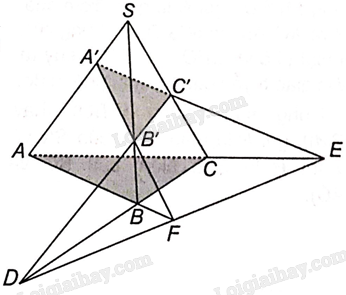
B’C’ và BC cắt nhau tại D nên D nằm trên giao tuyến của hai mặt phẳng (A’B’C’) và (ABC).
C’A’ và CA cắt nhau tại E nên E nằm trên giao tuyến của hai mặt phẳng (A’B’C’) và (ABC).
A’B’ và AB cắt nhau tại F nên F nằm trên giao tuyến của hai mặt phẳng (A’B’C’) và (ABC).
Vậy D, E, F cùng nằm trên giao tuyến của hai mặt phẳng (A’B’C’) và (ABC) nên ba điểm này thẳng hàng.
Xem thêm các bài giải SBT Toán lớp 11 Kết nối tri thức hay, chi tiết khác:
Bài 9: Các số đặc trưng đo xu thế trung tâm
Bài 10: Đường thẳng và mặt phẳng trong không gian
Bài 11: Hai đường thẳng song song