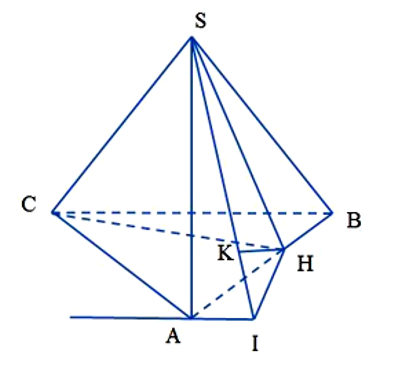
Cho hình chóp S.ABC có đáy là tam giác đều cạnh a. Hình chiếu vuông góc của S lên

Cho hình chóp S.ABC có đáy là tam giác đều cạnh a. Hình chiếu vuông góc của S lên mặt phẳng (ABC) là điểm H trên cạnh AB sao cho HA=2HB. Góc giữa SC mặt phẳng (ABC) bằng ${60}^0.$ Tính khoảng cách giữa hai đường thẳng SA và BC theo a. 

Trả lời

Chọn A.

Qua A kẻ đường thẳng d song song với BC. Gọi I là hình chiếu vuông góc của H lên d

$BC//\left(SAI\right)\Rightarrow d\left(BC,SA\right)=d\left(BC,\left(SAI\right)\right)=d\left(B,\left(SAI\right)\right)=\frac{3}{2}d\left(H,\left(SAI\right)\right).$

Gọi K là hình chiếu vuông góc của H lên SI

$AI\perp HI,AI\perp SH\Rightarrow AI\perp \left(SHI\right)\Rightarrow AI\perp HK.$

$\Rightarrow HK\perp \left(SAI\right)\Rightarrow d\left(H,\left(SAI\right)\right)=HK.$

$\widehat{HAI}={180}^0-\left({60}^0+{60}^0\right)={60}^0.$

Tam giác AIH vuông tại $I:IH=AH\sin {60}^0=\frac{a\sqrt{3}}{3}.$

$\widehat{\left(SC,\left(ABC\right)\right)}=\widehat{\left(SC,CH\right)}=\widehat{SCH}={60}^0.$

$C{H}^2=B{C}^2+B{H}^2-2BC.BH.\cos {60}^0=\frac{7a^2}{9}\Rightarrow CH=\frac{a\sqrt{7}}{3}.$

Tam giác SHC vuông tại $H:SH=HC.\tan {60}^0=\frac{a\sqrt{21}}{3}.$

Tam giác SHI vuông tại $H:\frac{1}{H{K}^2}=\frac{1}{S{H}^2}+\frac{1}{H{I}^2}\Rightarrow HK=\frac{a\sqrt{42}}{12}.$

$d\left(B,\left(SAI\right)\right)=\frac{3}{2}HK=\frac{a\sqrt{42}}{8}.$

Vậy $d\left(SA,BC\right)=\frac{a\sqrt{42}}{8}.$