Cho hình chóp S.ABC có SA ⊥ (ABC). Gọi α là số đo của góc nhị diện [A, BC, S]

Bài 6 trang 94 Toán 11 Tập 2: Cho hình chóp S.ABC có SA ⊥ (ABC). Gọi α là số đo của góc nhị diện [A, BC, S]. Chứng minh rằng tỉ số diện tích của hai tam giác ABC và SBC bằng cosα.

Trả lời

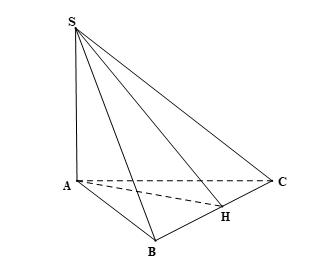
Kẻ AH ⊥ BC (H ∈ BC).

Vì SA ⊥ (ABC) và BC ⊂ (ABC) nên SA ⊥ BC.

Ta có: AH ⊥ BC, SA ⊥ BC và AH ∩ SA = A trong (SAH).

Suy ra BC ⊥ (SAH).

Mà SH ⊂ (SAH) nên BC ⊥ SH.

Ta có: AH ⊥ BC, SH ⊥ BC và AH ∩ SH = H ∈ BC.

Suy ra $\widehat{SHA}$ là góc phẳng nhị diện của góc nhị diện [A, BC, S], tức $\widehat{SHA}=\alpha .$

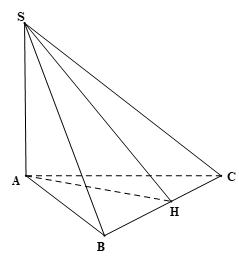
Vì SA ⊥ (ABC) và AH ⊂ (ABC) nên SA ⊥ AH.

Xét tam giác SAH vuông tại A (do SA ⊥ AH) có:

$\cos \alpha =\cos \widehat{SHA}=\frac{AH}{SH}.$

Diện tích tam giác ABC (có AH ⊥ BC) là: $S_{\Delta ABC}=\frac{1}{2}AH.BC.$

Diện tích tam giác SBC (có SH ⊥ BC) là: $S_{\Delta SBC}=\frac{1}{2}SH.BC.$

$\Rightarrow \frac{S_{\Delta ABC}}{S_{\Delta SBC}}=\frac{\frac{1}{2}AH.BC}{\frac{1}{2}SH.BC}=\frac{AH}{SH}=\cos \widehat{SHA}=\cos \alpha .$

Vậy tỉ số diện tích của hai tam giác ABC và SBC bằng cosα.

Xem thêm các bài giải SGK Toán lớp 11 Cánh diều hay, chi tiết khác: