Câu hỏi:
03/04/2024 42
Cho hình chóp ABCD có đáy ABC là tam giác đều cạnh a. Gọi O là tâm đường tròn ngoại tiếp tam giác ABC. Biết . Gọi M là điểm thuộc đường cao AH của tam giác ABC. Xét mặt phẳng (P) đi qua M và vuông góc với . Xác định vị trí điểm M để thiết diện của hình chóp cắt bởi mặt phẳng (P) có điện tích lớn nhất. Khi đó bằng:
Cho hình chóp ABCD có đáy ABC là tam giác đều cạnh a. Gọi O là tâm đường tròn ngoại tiếp tam giác ABC. Biết . Gọi M là điểm thuộc đường cao AH của tam giác ABC. Xét mặt phẳng (P) đi qua M và vuông góc với . Xác định vị trí điểm M để thiết diện của hình chóp cắt bởi mặt phẳng (P) có điện tích lớn nhất. Khi đó bằng:
A.
B.
C.
D.
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Lời giải
Chọn C
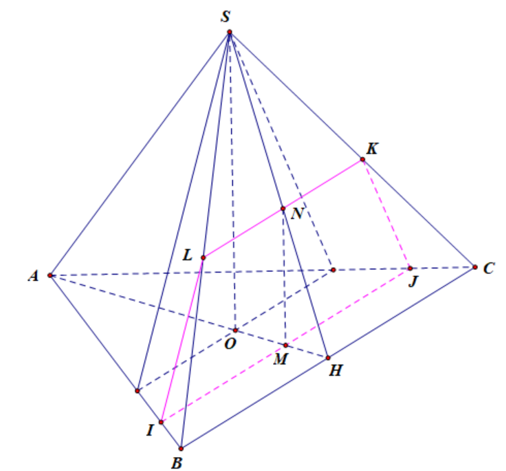
Do nên thiết diện là hình thang cân IJKL có đường cao .
Do nên M nằm giữa O,H.
..
.
khi .
Lời giải
Chọn C

Do nên thiết diện là hình thang cân IJKL có đường cao .
Do nên M nằm giữa O,H.
..
.
khi .
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Cho hình chóp SABC có SA=SC=AB=AC= và BC=2a. Khi đó góc giữa hai đường thẳng AC và SB.
Cho hình chóp SABC có SA=SC=AB=AC= và BC=2a. Khi đó góc giữa hai đường thẳng AC và SB.
Câu 3:
Cho f(x) liên tục trên [-1,5] thỏa mãn f(-1)=1, f(5)= 6. Phương trình nào sau đây luôn có nghiệm trong khoảng (1,-5) ?
Cho f(x) liên tục trên [-1,5] thỏa mãn f(-1)=1, f(5)= 6. Phương trình nào sau đây luôn có nghiệm trong khoảng (1,-5) ?
Câu 8:
Cho hình chóp SABCD có đáy ABCD là hinh thoi tâm O . Biết SA=SC, SB=SD. Khẳng định nào sau đây sai?
Câu 11:
Cho hình chóp SABC có và . H là hình chiếu vuông góc của A lên SB. Khẳng định nào sau đây là đúng?
Cho hình chóp SABC có và . H là hình chiếu vuông góc của A lên SB. Khẳng định nào sau đây là đúng?
Câu 13:
Cho các khẳng định:
(I): Cho hàm số y= f(x) liên tục trên [a,b] và . Khi đó phương trình có ít nhất một nghiệm trên khoảng (a,b).
(II): Cho hàm số liên tục trên [a,b] và . Khi đó phương trình f(x)=0 không có nghiệm trên khoảng (a,b).
Trong các khẳng định trên:
Cho các khẳng định:
(I): Cho hàm số y= f(x) liên tục trên [a,b] và . Khi đó phương trình có ít nhất một nghiệm trên khoảng (a,b).
(II): Cho hàm số liên tục trên [a,b] và . Khi đó phương trình f(x)=0 không có nghiệm trên khoảng (a,b).
Trong các khẳng định trên:
Câu 14:
Cho hình hộp ABCDA'B'C'D'. Một đường thẳng cắt các đường thẳng AA', BC, C'D' lần lượt tại M, N,P sao cho . Tính ?
Cho hình hộp ABCDA'B'C'D'. Một đường thẳng cắt các đường thẳng AA', BC, C'D' lần lượt tại M, N,P sao cho . Tính ?


