Cho hình bình hành ABCD có AB = 2AD. Gọi E và F lần lượt là trung điểm của AB và CD

Bài 11 trang 89 Toán 8 Tập 1: Cho hình bình hành ABCD có AB = 2AD. Gọi E và F lần lượt là trung điểm của AB và CD, I là giao điểm của AF và DE, K là giao điểm của BF và CE.

a) Chứng minh rằng tứ giác AECF là hình bình hành.

b) Tứ giác AEFD là hình gì? Vì sao?

c) Chứng minh rằng tứ giác EIFK là hình chữ nhật.

d) Tìm điều kiện của hình bình hành ABCD để tứ giác EIFK là hình vuông.

Trả lời

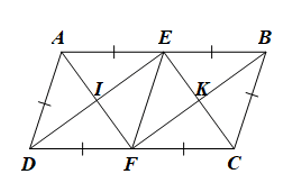
a) • Do ABCD là hình bình hành nên AB = CD và AB // CD.

Vì E là trung điểm của AB nên $EA=EB=\frac{1}{2}AB$.

     F là trung điểm của CD nên $FC=FD=\frac{1}{2}CD$.

Mà AB = CD (chứng minh trên).

Do đó EA = EB = FC = FD.

• Xét tứ giác AECF có EA = FC và EA // FC (do AB // CD)

Suy ra AECF là hình bình hành.

b) Xét tứ giác AEFD có AE = DF (chứng minh ở câu a) và AE // DF (do AB // CD)

suy ra AEFD là hình bình hành.

Mặt khác AB = 2AD nên $AD=AE=\frac{1}{2}AB$

Khi đó hình bình hành AEFD là hình thoi.

c) Do AEFD là hình thoi (câu c) nên ta có:

• AF ⊥ DE suy ra $\widehat{EIF}=90°$;

• ED là đường phân giác của góc AEF nên $\widehat{DEF}=\frac{1}{2}\widehat{AEF}$.

Chứng minh tương tự câu c ta cũng có tứ giác BEFC là hình thoi

Suy ra:

• BF ⊥ CE suy ra $\widehat{EKF}=90°$;

• EC là đường phân giác của góc BEF nên $\widehat{CEF}=\frac{1}{2}\widehat{BEF}$.

Ta có: $\widehat{IEK}=\widehat{DEF}+\widehat{CEF}=\frac{1}{2}\widehat{AEF}+\frac{1}{2}\widehat{BEF}=\frac{1}{2}\left(\widehat{AEF}+\widehat{BEF}\right)$

Mà $\widehat{AEF}+\widehat{BEF}=180°$ (hai góc kể bù)

Suy ra $\widehat{IEK}=\widehat{DEF}+\widehat{CEF}=\frac{1}{2}.180°=90°$.

• Xét tứ giác EIFK có $\widehat{EIF}=90°;\widehat{EKF}=90°;\widehat{IEK}=90°$ nên là hình chữ nhật.

d) Theo câu c, tứ giác EIFK là hình chữ nhật

Do đó để tứ giác EIFK là hình vuông thì IE = IF   (1)

Xét hình thoi AEFD có hai đường chéo AF, DE cắt nhau tại trung điểm của mỗi đường nên I là trung điểm của AF và DE.

Suy ra IA = IF và ID = IE (2)

Từ (1) và (2) suy ra IA = ID

Tam giác IAD có IA = ID nên là tam giác cân tại I

Lại có $\widehat{AID}=90°$ (do AF ⊥ DE) nên DIAD vuông cân tại I

Suy ra $\widehat{IAD}=45°$.

Mặt khác AEFD là hình thoi (câu c) nên ta có AF là đường phân giác của góc EAD

Suy ra $\widehat{EAD}=2\widehat{IAD}=2.45°=90°$, hay $\widehat{BAD}=90°$.

Vậy để tứ giác EIFK là hình vuông thì hình bình hành ABCD cần thêm điều kiện $\widehat{BAD}=90°$ hay ABCD là hình chữ nhật.

Xem thêm lời giải bài tập SGK Toán lớp 8 Chân trời sáng tạo hay, chi tiết khác:

Bài 4: Hình bình hành – Hình thoi

Bài 5: Hình chữ nhật – Hình vuông

Bài tập cuối chương 3