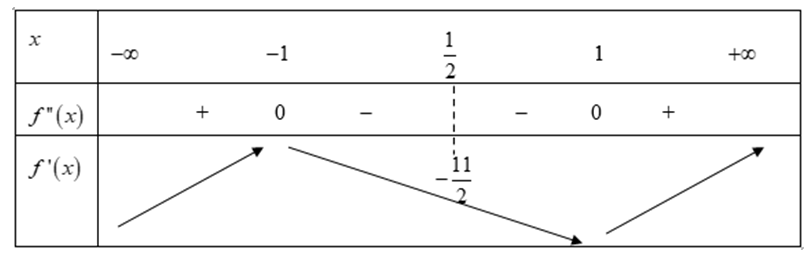
Cho hàm số y= f(x) và f(x)> 0, với mọi x thuộc R. Biết hàm số y= f'(x) có bảng biên thiên

Cho hàm số y= f(x) và $f\left(x\right)>0,\forall x\in ℝ.$ Biết hàm số y= f'(x) có bảng biên thiên như hình vẽ và $f\left(\frac{1}{2}\right)=\frac{137}{16}.$

Có bao nhiêu giá trị nguyên của $m\in \left[-2020;2020\right]$ để hàm số $g\left(x\right)=e^{-x^2+4mx-5}.f\left(x\right)$ đồng biến trên $\left(-1;\frac{1}{2}\right).$ 

Trả lời

Chọn B.

Ta có: $g\text{'}\left(x\right)=\left(-2x+4m\right).e^{-x^2+4mx-5}.f\left(x\right)+e^{-x^2+4mx-5}.f\text{'}\left(x\right)$

$\iff g\text{'}\left(x\right)=\left[\left(-2x+4m\right).f\left(x\right)+f\text{'}\left(x\right)\right].e^{-x^2+4mx-5}.$

Yêu cầu bài toán $\iff g\text{'}\left(x\right)\ge 0,\forall x\in \left(-1;\frac{1}{2}\right)$ và g'(x) = 0 chỉ xảy ra tại một số hữu hạn điểm thuộc $\left(-1;\frac{1}{2}\right).$

$\iff \left(-2x+4m\right).f\left(x\right)+f\text{'}\left(x\right)\ge 0,\forall x\in \left(-1;\frac{1}{2}\right)$ (vì $e^{-x^2+4mx-5}>0)$

$\iff -2x+4m\ge -\frac{f\text{'}\left(x\right)}{f\left(x\right)},\forall x\in \left(-1;\frac{1}{2}\right),$ (vì $f\left(x\right)>0,\forall x\in ℝ)$

$\iff 4m\ge 2x-\frac{f\text{'}\left(x\right)}{f\left(x\right)},\forall x\in \left(-1;\frac{1}{2}\right)\left(*\right).$

Xét $h\left(x\right)=2x-\frac{f\text{'}\left(x\right)}{f\left(x\right)},\forall x\in \left(-1;\frac{1}{2}\right).$ Ta có $h\text{'}\left(x\right)=2-\frac{f"\left(x\right).f\left(x\right)-{\left[f\text{'}\left(x\right)\right]}^2}{f^2\left(x\right)}.$

Mà $\left\{\begin{array}{l}f"\left(x\right)<0\\ f\left(x\right)>0\end{array}\right.,\forall x\in \left(-1;\frac{1}{2}\right)\Rightarrow \frac{f"\left(x\right).f\left(x\right)-{\left[f\text{'}\left(x\right)\right]}^2}{f^2\left(x\right)}<0,\forall x\in \left(-1;\frac{1}{2}\right).$

Từ đó suy ra $h\text{'}\left(x\right)>0,\forall x\in \left(-1;\frac{1}{2}\right).$ Vậy hàm số h(x) đồng biến trên $\left(-1;\frac{1}{2}\right).$

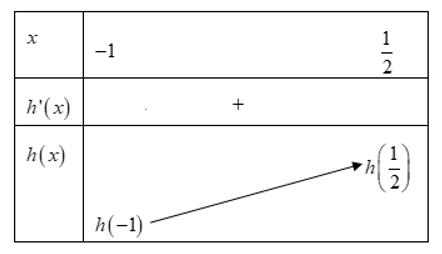
Bảng biến thiên:

Vậy điều kiện $\left(*\right)\iff 4m\ge h\left(\frac{1}{2}\right)\iff 4m\ge 2.\left(\frac{1}{2}\right)-\frac{f\text{'}\left(\frac{1}{2}\right)}{f\left(\frac{1}{2}\right)}\iff 4m\ge \frac{225}{137}\iff m\ge \frac{225}{548}.$

Lại có $\left\{\begin{array}{l}m\in \mathbb{Z}\\ m\in \left[-2020;2020\right]\end{array}\right.\Rightarrow m\in \left\{1;2;3;\mathrm{...};2020\right\}.$

Vậy có 2020 giá trị nguyên của m thỏa mãn yêu cầu bài toán.