Cho hàm số y= f(x) liên tục trên R có đồ thị như hình vẽ. Phương trình f(2-f(x))=0 có tất cả
100
23/04/2024
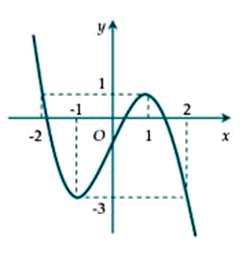
Cho hàm số y= f(x) liên tục trên R có đồ thị như hình vẽ.
Phương trình f(2−f(x))=0 có tất cả bao nhiêu nghiệm thực phân biệt?
A. 7
B. 4.
C. 6.
D. 5
Trả lời
Chọn D.
Xét phương trình: f(2−f(x))=0. Đặt u=2−f(x).
Phương trình trở thành: f(u)=0
Dựa vào đồ thị ta thấy:
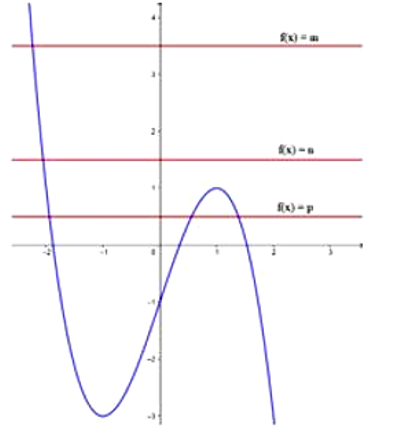
f(u)=0⇔[u=a(a∈(−2;−1))u=b(b∈(0;1))u=c(c∈(1;2))⇔[f(x)=2−a=m(m∈(3;4))f(x)=2−b=n(n∈(1;2))f(x)=2−c=p(p∈(0;1))
Với f(x)=m(m∈(3;4)) phương trình có 1 nghiệm duy nhất.
Với f(x)=n(n∈(1;2)) phương trình có 1 nghiệm duy nhất.
Với f(x)=p(p∈(0;1)) phương trình có 3 nghiệm phân biệt.
Vậy phương trình f(2−f(x))=0 có tất cả 5 nghiệm thực phân biệt.