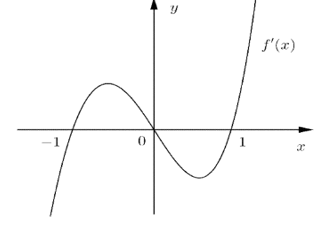
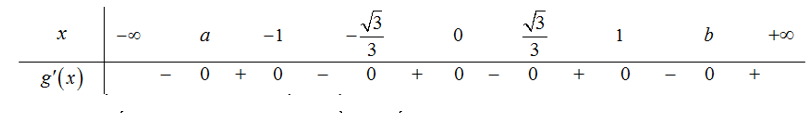Cho hàm số y= f(x), hàm số f'(x)= x^3+ ax^2+bx+ c( a,b,c thuộc R) có đồ thị như hình vẽ
30
29/04/2024
Cho hàm số y= f(x), hàm số có đồ thị như hình vẽ
Hàm số có mấy khoảng đồng biến?
A. 4.
B. 3.
C. 2.
D. 1.
Trả lời
Chọn A
Dựa vào đồ thị ta có :
.
Khi đó
Ta có .
Xét .
Xét .
Với .
Ta có .
Do đó .
Các nghiệm của phương trình đều là các nghiệm đơn nên áp dụng quy tắc đan dấu, ta có bảng biến thiên như sau :
Vậy hàm số đã cho có 4 khoảng đồng biến.